
【题目】如图,在△ABC中,点D.E分别在边AB,AC上,DE∥BC,按下列要求画图并填空
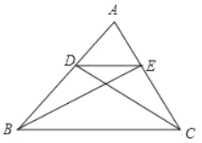
(1)过点E画直线BC的垂线交直线BC于点F;
(2)点D到直线______的距离等于线段EF的长度
(3)联结BE.CD,EBC的面积______DBC的面积.
科目:初中数学 来源: 题型:
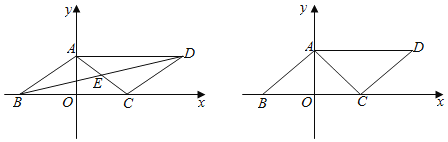
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过点D的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG,EF.

(1)说明:BG=CF;
(2)BE,CF与EF这三条线段能否组成一个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字后,回答问题:
甲、乙两人同时解答题目:“化简并求值:![]() ,其中a=5.”甲、乙两人的解答不同;
,其中a=5.”甲、乙两人的解答不同;
甲的解答是:![]() ;
;
乙的解答是:![]() .
.
(1) 的解答是错误的.
(2)错误的解答在于未能正确运用二次根式的性质: .
(3)模仿上题解答:化简并求值:![]() ,其中a=2.
,其中a=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD边BC在x轴上,顶点A在y轴上,对角线AC所在的直线为y=![]() +6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
+6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
(1)直接写出顶点D的坐标(______,______),对角线的交点E的坐标(______,______);
(2)求对角线BD的长;
(3)是否存在t,使S△POQ=![]() SABCD,若存在,请求出的t值;不存在说明理由.
SABCD,若存在,请求出的t值;不存在说明理由.
(4)在整个运动过程中,PQ的中点到原点O的最短距离是______cm,(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
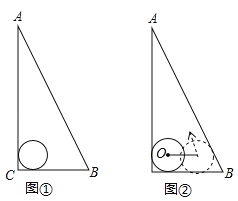
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=﹣![]() ,x1x2=
,x1x2=![]() (说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=![]() ,x1x2=﹣
,x1x2=﹣![]() ,请根据阅读材料解答下列各题:
,请根据阅读材料解答下列各题:
(1)已知方程x2﹣3x﹣2=0的两根为x1、x2,且x1>x2,求下列各式的值:
①x12+x22;②![]() ;
;
(2)已知x1,x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
②求使![]() 的值为整数的实数k的整数值.
的值为整数的实数k的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小明此时与地面的垂直距离CD的值;
(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
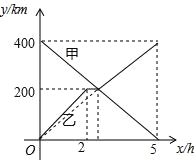
(1)乙车休息了 h.
(2)求乙车与甲车相遇后y乙关于x的函数表达式,并写出自变量x的取值范围.
(3)当两车相距40km时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com