
【题目】如图,已知□ABCD边BC在x轴上,顶点A在y轴上,对角线AC所在的直线为y=![]() +6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
+6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
(1)直接写出顶点D的坐标(______,______),对角线的交点E的坐标(______,______);
(2)求对角线BD的长;
(3)是否存在t,使S△POQ=![]() SABCD,若存在,请求出的t值;不存在说明理由.
SABCD,若存在,请求出的t值;不存在说明理由.
(4)在整个运动过程中,PQ的中点到原点O的最短距离是______cm,(直接写出答案)
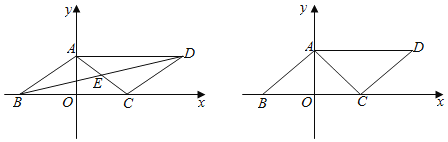
【答案】(1)16;6;4;3;(2)BD=6![]() ;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为
;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为![]() .
.
【解析】
(1)令x=0,y=0代入解析式得出A,C坐标,进而利用平行四边形的性质解答即可;
(2)根据平行四边形的性质得出点B,D坐标,利用两点间距离解答即可;
(3)利用三角形的面积公式和平行四边形的面积公式列出方程解答即可;
(4)根据直角三角形斜边上中线等于斜边的一半可知,当PQ长度最短时,PQ的中点到原点O的距离最短解答即可.
(1)把x=0代入y=![]() +6,可得y=6,
+6,可得y=6,
即A的坐标为(0,6),
把y=0代入y=![]() +6,可得:x=8,
+6,可得:x=8,
即点C的坐标为(8,0),
根据平行四边形的性质可得:点B坐标为(-8,0),
所以AD=BC=16,
所以点D坐标为(16,6),
点E为对角线的交点,
故点E是AC的中点,
E的坐标为(4,3),
故答案为:16;6;4;3;
(2)因为B(-8,0)和D(16,6),
∴BD=![]() ;
;
(3)设时间为t,可得:OP=6-t,OQ=8-2t,
∵S△POQ= SABCD,
当0<t≤4时,![]() ,
,
解得:t1=2,t2=8(不合题意,舍去),
当4<t≤6时,![]() ,
,
△<0,不存在,
答:存在S△POQ=![]() SABCD,此时t值为2;
SABCD,此时t值为2;
(4)∵![]() ,
,
当t=![]() 时,PQ=
时,PQ=![]() ,
,
当PQ长度最短时,PQ的中点到原点O的距离最短,此时PQ的中点到原点O的最短距离为![]() PQ=
PQ=![]()
![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)6a2-5a(a+2b-1)+a(-a+10b)+5,其中a=-1,b=2008;
(2)3xy2﹣[xy﹣2(2xy﹣![]() x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取1 000户家庭调查;
B.从一个城镇的不同住宅楼中随机选取1 000户家庭调查;
C.从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.
(1)在上述调查方式中,你认为比较合理的一个是【1】.(填“A”、“B”或“C”)
(2)将一种比较合理的调查方式调查得到的结果分为四类:(A)已有两个孩子;
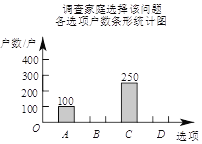
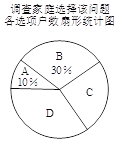
(B)决定生二胎;(C)考虑之中;(D)决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
①补全条形统计图.
②估计该市100万户家庭中决定不生二胎的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
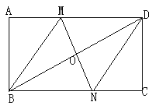
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
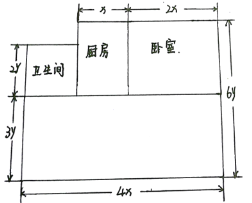
【题目】如图是一套房子的平面图,尺寸如图.
(1)这套房子的总面积是多少?(用含x、y的代数式表示)
(2)如果x=1.8米,y=1米,那么房子的面积是多少平方米?如果每平方米房价为5万元,那么房屋总价多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D.E分别在边AB,AC上,DE∥BC,按下列要求画图并填空
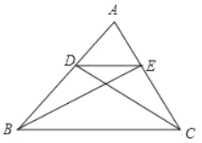
(1)过点E画直线BC的垂线交直线BC于点F;
(2)点D到直线______的距离等于线段EF的长度
(3)联结BE.CD,EBC的面积______DBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期五晚上,小明和他的妈妈一起看《歌手》,歌手演唱完后要评选出名次,在已公布四到七名后,还有华晨宇、汪峰、张韶涵三位选手没有公布名次.
(1)求汪峰获第一名的概率;
(2)如果小明和妈妈一起竞猜第一名,那么两人中一个人猜中另一个人却没猜中的概率是多少?(请用“树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?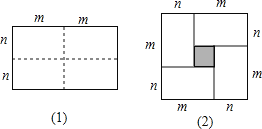
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com