
科目: 来源: 题型:
【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一副三角板按如图1方式拼接在一起,其中边![]() ,
,![]() 与直线
与直线![]() 重合,
重合,![]() ,
,![]() .
.

(1)图 1 中,![]() =______°.
=______°.
(2)如图2,三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线
,在转动过程中两块三角板都在直线![]() 的上方:
的上方:
①当![]() 平分
平分![]() 、
、![]() 、
、![]() 其中的两边组成的角时,求满足要求的所有旋转角度
其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
②是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校开展“校园献爱心”活动.准备向西部山区学校捐赠男、女两种款式的书包,已知男款书包单价![]() 元/个,女款书包单价
元/个,女款书包单价![]() 元/个.
元/个.
![]() 原计划募捐
原计划募捐![]() 元,恰好可购买两种款式的书包
元,恰好可购买两种款式的书包![]() 个,问两种款式的书包各买多少个?
个,问两种款式的书包各买多少个?
![]() 在捐款活动中,师生积极性高,实际捐款额和书包数量都高于原计划.快递公司将这些书包装箱运送,其中每箱书包数量相同.第一次他们领走这批的
在捐款活动中,师生积极性高,实际捐款额和书包数量都高于原计划.快递公司将这些书包装箱运送,其中每箱书包数量相同.第一次他们领走这批的![]() ,结果装了
,结果装了![]() 箱还多
箱还多![]() 个书包;第二次他们把余下的
个书包;第二次他们把余下的![]() 领走.连同第一次装箱剩下的
领走.连同第一次装箱剩下的![]() 个书包一起,刚好装了
个书包一起,刚好装了![]() 箱.问:实际购买书包共多少个?
箱.问:实际购买书包共多少个?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
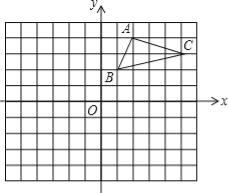
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
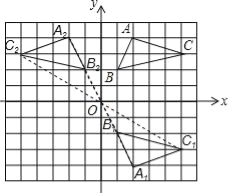
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=x﹣2与反比例函数y=![]() (x>0)的图象相交于点M(m,1).
(x>0)的图象相交于点M(m,1).
(1)填空:m的值为 ,反比例函数的解析式为 ;
(2)已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y=![]() (x>0)的图象与点B,试用n表示△NAB的面积S.
(x>0)的图象与点B,试用n表示△NAB的面积S.

查看答案和解析>>
科目: 来源: 题型:
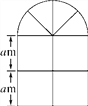
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com