
科目: 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于点A(![]() ,
, ![]() ),B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
),B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】一家商店因换季将某种服装打折销售,每件服装如果按标价的4折出售将亏40元,而按标价8折出售将赚40元.问:
(1)每件服装的标价是多少元?
(2)每件服装的成本是多少元?
(3)为了保证不亏损,最多可以打几折?
查看答案和解析>>
科目: 来源: 题型:
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |

请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?
查看答案和解析>>
科目: 来源: 题型:
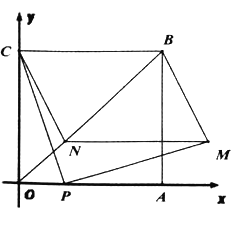
【题目】如图,在四边形![]() 是边长为4的正方形点P为OA边上任意一点(与点
是边长为4的正方形点P为OA边上任意一点(与点![]() 不重合),连接CP,过点P作
不重合),连接CP,过点P作![]() ,且
,且![]() ,过点M作
,过点M作![]() ,交
,交![]() 于点
于点![]() 联结
联结![]() ,设
,设![]() .
.
(1)当![]() 时,点
时,点![]() 的坐标为( , )
的坐标为( , )
(2)设![]() ,求出
,求出![]() 与
与![]() 的函数关系式,写出函数的定义域。
的函数关系式,写出函数的定义域。
(3)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用
的坐标(用![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右平移2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标.
(3)观察△A1B1C1和△A2B2C2,它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() 与
与![]() 互为相反数.
互为相反数.
![]()
(1)![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数_________表示的点重合;
与数_________表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒2个单位长度的速度向左运动,同时,点
以每秒2个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒1个单位长度和3个单位长度的速度向右运动,假设
分别以每秒1个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请问:
,请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 坐标为( , ),B为( , ).
坐标为( , ),B为( , ).
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,若四边形
,若四边形![]() 是平行四边形时,求出此时
是平行四边形时,求出此时![]() 的值.
的值.
(3)若点![]() 为
为![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,则在轴上是否存在一点
,则在轴上是否存在一点![]() ,使得
,使得![]() 四个点能构成一个梯形若存在,求出所有符合条件的
四个点能构成一个梯形若存在,求出所有符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分6分)如图所示的方格地面上,标有编号1、2、3的3
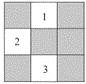
个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地
面完全相同.
(1)一只自由飞行的小鸟,将随意地落在图中所示的方格地面上,求
小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,
则编号为1、2的2个小方格空地种植草坪的概率是多少(用树状图或列表法求解)?
查看答案和解析>>
科目: 来源: 题型:
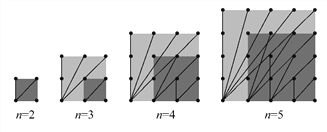
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com