
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,a),B(b,12-b),C(2a-3,0),0<a<b<12,若OB平分∠AOC,且AB=BC,则a+b的值为( )
A. 9或12B. 9或11C. 10或11D. 10或12
查看答案和解析>>
科目: 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目: 来源: 题型:
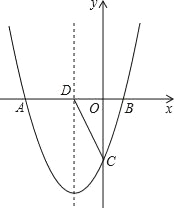
【题目】如图,抛物线y1=![]() 2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2
2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2![]() ),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
(1)求抛物线y1的解析式;
(2)将△OCD沿CD翻折后,O点对称点O′是否在抛物线y1上?请说明理由.
(3)若点E关于直线CD的对称点E′恰好落在x轴上,过E′作x轴的垂线交抛物线y1于点F,①求点F的坐标;②直线CD上是否存在点P,使|PE﹣PF|最大?若存在,试写出|PE﹣PF|最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】【阅读发现】如图①,在正方形ABCD的外侧,作两个等边三角形ABE和ADF,连结ED与FC交于点M,则图中△ADE≌△DFC,可知ED=FC,求得∠DMC= .
【拓展应用】如图②,在矩形ABCD(AB>BC)的外侧,作两个等边三角形ABE和ADF,连结ED与FC交于点M.

(1)求证:ED=FC.
(2)若∠ADE=20°,求∠DMC的度数.
查看答案和解析>>
科目: 来源: 题型:
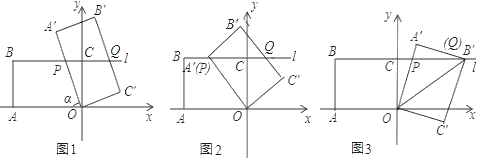
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A(﹣4,0),直线l∥x轴,交y轴于点C(0,3),点B(﹣4,3)在直线l上,将矩形OABC绕点O按顺时针方向旋转α度,得到矩形OA′B′C′,此时直线OA′、B′C′分别与直线l相交于点P、Q.
(1)当α=90°时,点B′的坐标为 .
(2)如图2,当点A′落在l上时,点P的坐标为 ;
(3)如图3,当矩形OA′B′C′的顶点B′落在l上时.
①求OP的长度;②S△OPB′的值是 .
(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能否成为平行四边形?如果能,请直接写出点B′和点P的坐标;如果不能,请简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定搞错了.”
(1)王老师为什么说他搞错了?试用方程的知识给予解释;
(2)陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本.但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,笔记本的单价可能为多少元?
查看答案和解析>>
科目: 来源: 题型:
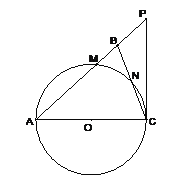
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com