
科目: 来源: 题型:
【题目】阅读下列材料: 1×2=![]() (1×2×3-0×1×2),2×3=
(1×2×3-0×1×2),2×3=![]() (2×3×4-1×2×3),3×4=
(2×3×4-1×2×3),3×4=![]() (3×4×5- 2×3×4),
(3×4×5- 2×3×4),
由以上三个等式左、右两边分别相加,可得:
1×2+2×3+3×4=![]() ×3×4×5=20
×3×4×5=20
读完以上材料,请你计算下列各题(写出过程):
(1)1×2+2×3+3×4+…+10×11= ;
(2)1×2+2×3+3×4+…+n×(n+1)= .
查看答案和解析>>
科目: 来源: 题型:
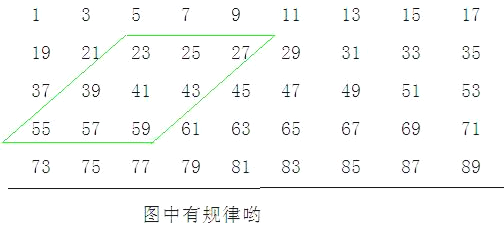
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知α+β=1,αβ=﹣1.设S1=α+β,S2=α2+β2,S3=α3+β3,…,Sn=αn+βn,
(1)计算:S1= ,S2= ,S3= ,S4= ;
(2)试写出Sn﹣2、Sn﹣1、Sn三者之间的关系;
(3)根据以上得出结论计算:α7+β7.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线y=2x-7平移后的图象l经过点(-3,-2),
(1)求l的函数解析式;并画出该函数的图象;
(2)l与x轴交于点A,点P是l上一点,且S△AOP=![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
![]()
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目: 来源: 题型:
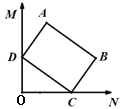
【题目】如图,∠MON=90°,矩形ABCD的顶点C、D分别在边ON,OM上滑动,AB=9,BC=6,在滑动过程中,点A到点O的最大距离为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点(x1,y1),(x2,y2),(x3,y3)都在函数y=-2x+7的图象上,若数据x1,x2,x3的方差为5,则另一组数据y1,y2,y3的方差为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com