
科目: 来源: 题型:
【题目】某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
数据收集 | 10 | 9.5 | 9.5 | 10 | 8 | 9 | 9.5 | 9 | 7 | 10 | 4 | 5.5 | 10 | 7.9 | 9.5 | 10 |
数据分析 | 9.5 | 9 | 8.5 | 8.5 | 10 | 9.5 | 10 | 8 | 6 | 9.5 | 10 | 9.5 | 9 | 8.5 | 9.5 | 6 |
整理,描述数据:按如下分数段整理,描述这两组样本数据:
|
|
|
| 10 | |
数据收集 | 1 | 1 | 3 | 6 | 5 |
数据分析 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据:两组样本数据的平均数,中位数,众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
数据收集 | 8.75 | 9.5 | 10 |
数据分析 | 8.81 | 9.25 | 9.5 |
得出结论:
(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;
(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目: 来源: 题型:
【题目】探究:如图①,AB∥CD∥EF,点G、P、H分别在直线AB、CD、EF上,连结PG、PH,当点P在直线GH的左侧时,试说明∠AGP+∠EHP=∠GPH.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).

解:如图①,∵AB∥CD( )
∴∠AGP=∠GPD
∵CD∥EF
∴∠DPH=∠EHP( )
∵∠GPD+∠DPH=∠GPH,
∴∠AGP+∠EHP=∠GPH( )
拓展:将图①的点P移动到直线GH的右侧,其他条件不变,如图②.试探究∠AGP、∠EHP、∠GPH之间的关系,并说明理由.
应用:如图③,AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ= 度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A、B、C在同一直线上,M、N分别是AB,BC的中点.
(1)若AB=20,BC =8,求MN的长;
(2)若AB =a,BC =8,求MN的长;
(3)若AB =a,BC =b,求MN的长;
(4)从(1)(2)(3)的结果中能得到什么结论?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
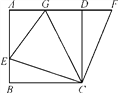
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?

查看答案和解析>>
科目: 来源: 题型:
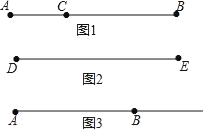
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作对角线BD的垂线,垂足为E,点F为AD的中点,连接FE并延长交BC于点G.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求BG的长.
,求BG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
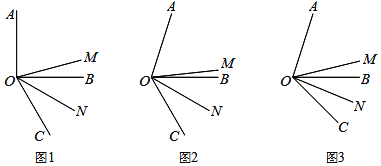
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= 度.(直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON的度数是多少?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 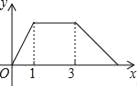
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com