
科目: 来源: 题型:
【题目】某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)分别求出两种优惠方案中y与x之间的关系式;
(2)购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】安岳是有名的“柠檬之乡”,某超市用3000元进了一批柠檬销售良好;又用7700元购来一批柠檬,但这次的进价比第一批高了10%,购进数量是第一批的2倍多500斤.
(1)第一批柠檬的进价是每斤多少元?
(2)为获得更高利润,超市决定将第二批柠檬分成大果子和小果子分别包装出售,大果子的售价是第一批柠檬进价的2倍,小果子的售价是第一批柠檬进价的1.2倍.问大果子至少要多少斤才能使第二批柠檬的利润不低于3080元?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列解题过程,并解答后面的问题:
如图,在平面直角坐标系中,![]() ,
,![]() ,C为线段AB的中点,求C的坐标.解:分别过A,C作x轴的平行线,过B,C作y轴的平行线,两组平行线的交点如图1.
,C为线段AB的中点,求C的坐标.解:分别过A,C作x轴的平行线,过B,C作y轴的平行线,两组平行线的交点如图1.
设C的坐标为![]() ,则D、E、F的坐标为
,则D、E、F的坐标为![]() ,
,![]() ,
,![]()
由图可知:![]() ,
,![]()
∴C的坐标为![]()
问题:
(1)已知A(-1,4),B(3,-2),则线段AB的中点坐标为______
(2)平行四边形ABCD中,点A、B、C的坐标分别为(1,-4),(0,2),(5,6),求D的坐标.
(3)如图2,B(6,4)在函数![]() 的图象上,A的坐标为(5,2),C在x轴上,D在函数
的图象上,A的坐标为(5,2),C在x轴上,D在函数![]() 的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,点M、N是BC、CD边上的点,连接AM、BN,若BM=CN

(1)求证:AM⊥BN
(2)将线段AM绕M顺时针旋转90°得到线段ME,连接NE,试说明:四边形BMEN是平行四边形;
(3)将△ABM绕A逆时针旋转90°得到△ADF,连接EF,当![]()
![]() 时,请求出
时,请求出![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】一水池有两个进水口,一个出水口,一个水口在单位时间内的进、出水量如图(a)、(b)所示,某天从0点到6点,该水池的蓄水量如图(c)所示,给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点一定不进水不出水.则正确的论断是________.(填上所有正确论断的序号)
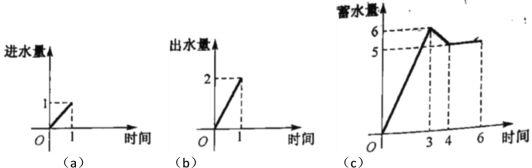
查看答案和解析>>
科目: 来源: 题型:
【题目】某物流公司的快递车和货车每天沿同一条路线往返于A、B两地,快递车比货车多往返一趟.如图所示,表示货车距离A地的路程y(单位:h)与所用时间x(单位h)的图像,其间在B地装卸货物2h.已知快递车比货车早1h出发,最后一次返回A地比货车晚1h.若快递车往返途中速度不变,且在A、B两地均不停留,则两车在往返途中相遇的次数为________次.
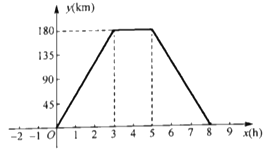
查看答案和解析>>
科目: 来源: 题型:
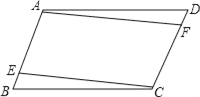
【题目】如图,四边形ABCD中,AD=BC,AB=CD,E,F分别是AB,CD上的点,且∠DAF=∠BCE,
(1)求证:AE=CF;
(2)若将此题中的条件改为:“E,F分别是AB,CD延长线上的点”,其余条件不变,此时,∠ABC=60°,∠BEC=40°,作∠ABC的平分线BN交AF于M,交AD于N,求∠AMN的度数(要求:画示意图,不写画法,写推理过程)
查看答案和解析>>
科目: 来源: 题型:
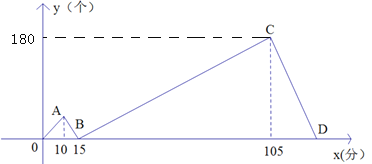
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com