
科目: 来源: 题型:
【题目】在一次禁毒宣传活动中,某执勤小组乘车沿东西向公路进行安全维护,如果约定向东为正,向西为负,行驶记录如下(单位:米):+18,-9,+7,-14,-3,+13,-8,-6,+15,+6.
(1)执勤过程中,最远处离出发点有多远?
(2)若汽车行驶每千米耗油量为![]() 升,求这次执勤的汽车共耗油多少升?
升,求这次执勤的汽车共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当-1≤x≤3时,y<0③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2④9a+3b+c=0其中正确的是( )
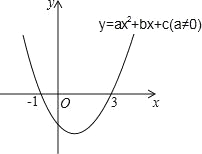
A.①②④ B.①④ C.①②③ D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】元旦那天,6位朋友均匀地围坐在圆桌旁共度佳节.如图,圆桌半径为60 cm,每人离圆桌的距离均为10 cm,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x,根据题意,可列方程( ).
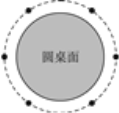
A. ![]() =
=![]()
B. ![]()
C. 2π(60+10)×6=2π(60+π)×8
D. 2π(60-x)×8=2π(60+x)×6
查看答案和解析>>
科目: 来源: 题型:
【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
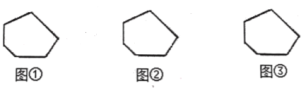
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割![]() 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含![]() 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,![]() 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形.
查看答案和解析>>
科目: 来源: 题型:
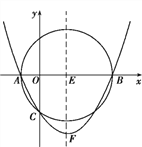
【题目】如图,已知以E(3,0)为圆心,5为半径的☉E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,顶点为F.
(1)求A,B,C三点的坐标;
(2)求抛物线的解析式及顶点F的坐标;
(3)已知M为抛物线上的一动点(不与C点重合),试探究:①若以A,B,M为顶点的三角形面积与△ABC的面积相等,求所有符合条件的点M的坐标;
②若探究①中的M点位于第四象限,连接M点与抛物线顶点F,试判断直线MF与☉E的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
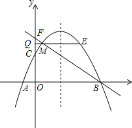
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,每个小方格都是边长为![]() 的正方形,
的正方形,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标是
的坐标是![]() .
.
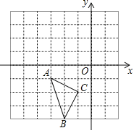
![]() 先将
先将![]() 沿
沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向向左平移
轴负方向向左平移![]() 个单位长度得到
个单位长度得到![]() ,画出
,画出![]() ,点
,点![]() 坐标是________;
坐标是________;
![]() 将
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,画出
,画出![]() ,并求出点
,并求出点![]() 的坐标是________;
的坐标是________;
![]() 我们发现点
我们发现点![]() 、
、![]() 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣和爱好情况,并根据调查结果制作了如下两幅统计图.

根据图中提供的信息解答下列问题:
(1)求本次抽样调查的人数;(要求列式计算,写出求解过程)
(2)补全人数统计图;
(3)“运动”对应的扇形的圆心角度数是 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com