
科目: 来源: 题型:
【题目】下列说法:
①连接两点间的线段叫这两点的距离;
②木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
③若![]() 三点在同一直线上,且
三点在同一直线上,且![]() ,则
,则![]() 是线段
是线段![]() 的中点;
的中点;
④若![]() ,则有
,则有![]() .
.
其中一定正确的是_________(把你认为正确结论的序号都填上) .
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y=ax2+bx+c (a,b,c为常数,且a≠0)经过点(﹣1,0)、(m,0),且1<m<2,当x<﹣1时,y随x增大而减小,下列结论:①abc>0;②a+b<0;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0;⑤c≤﹣1时,则b2﹣4ac≤4a.其中结论正确的有( )个
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】某班为了开展乒乓球比赛活动,准备购买一些乒乓球和乒乓球拍,通过去商店了解情况,甲乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价48元,乒乓球每盒定价12元,经商谈,甲乙两家商店给出了如下优惠措施:甲店每买一副乒乓球拍赠送一盒乒乓球,乙店全部按定价的9折优惠.现该班急需乒乓球拍5副,乒乓球![]() 盒(不少于5盒).
盒(不少于5盒).
(1)请用含![]() 的代数式分别表示去甲、乙两店购买所需的费用;
的代数式分别表示去甲、乙两店购买所需的费用;
(2)当需要购买40盒乒乓球时,通过计算,说明此时去哪家商店购买较为合算;
(3)当需要购买40盒乒乓球时,你能给出一种更为省钱的方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB点E,DF⊥BC于点F.将∠EDF绕点D顺时针旋转α°(0<α<180),其两边的对应边DE′、DF′分别与直线AB、BC相交于点G、P,如图2.连接GP,当△DGP的面积等于3![]() 时,则α的大小为( )
时,则α的大小为( )
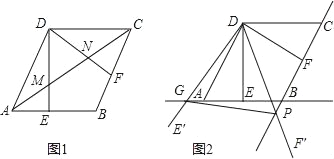
A. 30 B. 45 C. 60 D. 120
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=
BC,连接OE,下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB:④OE=![]() BC.其中成立的有( )
BC.其中成立的有( )

A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目: 来源: 题型:
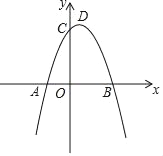
【题目】如图,已知抛物线y=ax2+2x+8与x轴交于A,B两点,与y轴交于点C,且B(4,0).
(1)求抛物线的解析式及其顶点D的坐标;
(2)如果点P(p,0)是x轴上的一个动点,则当|PC﹣PD|取得最大值时,求p的值;
(3)能否在抛物线第一象限的图象上找到一点Q,使△QBC的面积最大,若能,请求出点Q的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题背景:已知:如图①-1,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)
之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)

解:(1)![]() 与
与![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]() (或
(或![]() 只要关系式形式正确即可)
只要关系式形式正确即可)
理由:如图①-2,过点![]() 作
作![]() .
.
∵![]() (作图),
(作图),
∴![]() ( ),
( ),
∴![]() (已知)
(已知)
![]() (作图),
(作图),
∴![]() _______( ),
_______( ),
∴![]() _______( ),
_______( ),
∴![]() (等量代换)
(等量代换)
又∵![]() (角的和差),
(角的和差),
∴![]() (等量代换)
(等量代换)
总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.
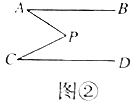
(2)类比探究:如图②,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() 、
、![]() ,请同学们类比(1)的解答过程,试探究
,请同学们类比(1)的解答过程,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.
之间有什么数量关系,并说明理由.
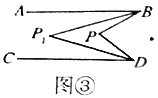
(3)拓展延伸:如图③,![]() ,
,![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数,请直接写出结果,不说明理由.
的度数,请直接写出结果,不说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
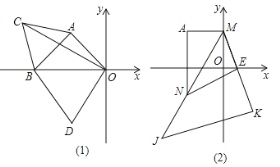
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,![]() 是直角,
是直角,![]() 在
在![]() 的外侧,且
的外侧,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
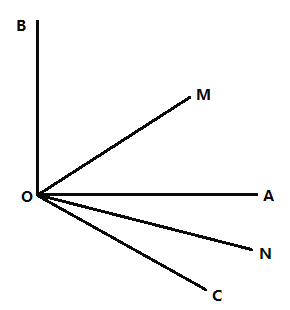
(1)求![]() 的大小;
的大小;
(2)当锐角![]() 的大小为
的大小为![]() 时,试猜想(1)中
时,试猜想(1)中![]() 的大小是否发生改变?并通过计算说明理由.
的大小是否发生改变?并通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com