
科目: 来源: 题型:
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证![]() ;
;
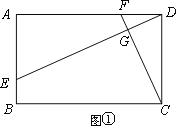


(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=4,DA=DC=6,∠BAD=90°,DE⊥CF,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
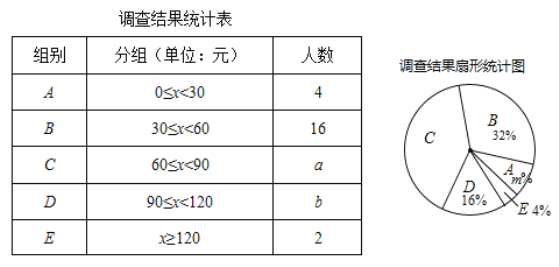
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__________人,a+b=__________,m=__________;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额在60≤x<120范围的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:抛物线![]() :
:![]() 与抛物线
与抛物线![]() 关于y轴对称, 抛物线
关于y轴对称, 抛物线![]() 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
(1)求b和m的值;
(2)求抛物线![]() 的解析式;
的解析式;
(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线![]() 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB =90°,AC = BC =2,AB =![]() ,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.
,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面上![]() 四个点.
四个点.

(1)按下列要求画图(不写画法)
①连接![]() ,
,![]() ;②作直线
;②作直线![]() ;③作射线
;③作射线![]() ,交
,交![]() 于点
于点![]() .
.
(2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段![]() ,
,![]() ,
,![]() ,可知
,可知![]() __________
__________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
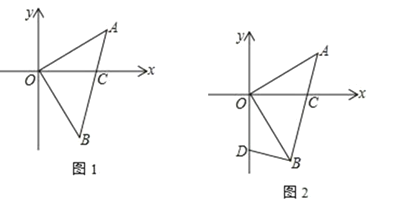
(1) 求△AOB的面积
(2) 如图2,点 D(0,![]() )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
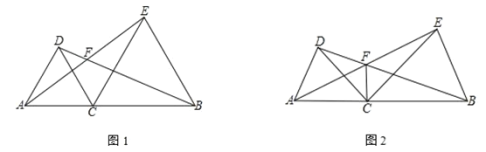
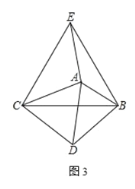
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AB=BC,D在边 AC上,AE⊥BD于 E
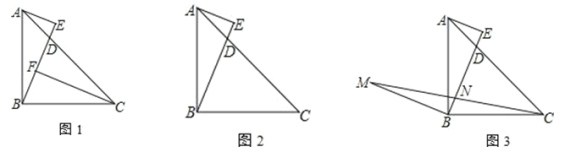
(1)如图1,作 CF⊥BD于F,求证:CF-AE=EF
(2)如图2,若 BC=CD,求![]() 的值
的值
(3)如图3,作 BM⊥BE,且 BM=BE,AE=2,EN=4,连 CM交 BE于 N,请直接写出△BCM的面积为___
查看答案和解析>>
科目: 来源: 题型:
【题目】探究活动:
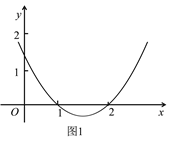
利用函数![]() 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
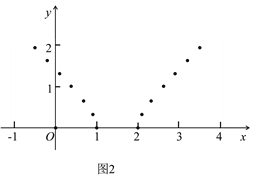
(2)如图2,小东列表描出了函数![]() 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;
(3)解决问题:设方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() ,方程
,方程
![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() .若
.若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接).
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
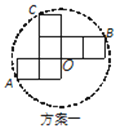
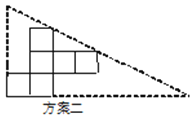
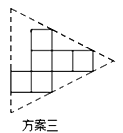
说明:方案一图形中的圆过点A,B,C,圆心O也是正方形的顶点;
回答问题(直接写出结果):
(1)方案二中,直角三角形纸片的两条直角边长分别为_______cm和_______cm;
(2)小明通过计算,发现方案一中纸片的利用率是________(填准确值),近似值约为38.2%.相比之下,方案二的利用率是________%.小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com