练习册

  • 练习册
  • 试题
    相关习题
     0  356294  356302  356308  356312  356318  356320  356324  356330  356332  356338  356344  356348  356350  356354  356360  356362  356368  356372  356374  356378  356380  356384  356386  356388  356389  356390  356392  356393  356394  356396  356398  356402  356404  356408  356410  356414  356420  356422  356428  356432  356434  356438  356444  356450  356452  356458  356462  356464  356470  356474  356480  356488  366461 

    科目： 来源： 题型：

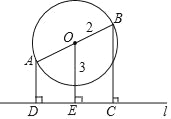
    【题目】如图，以AB为直径的⊙O的圆心O到直线l的距离OE=3，⊙O的半径r=2，直线AB不垂直于直线l，过点A，B分别作直线l的垂线，垂足分别为点D，C，则四边形ABCD的面积的最大值为__________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知：如图，在梯形 ABCD 中，AD∥BC，E 是 AB 的中点，CE 的延长线与 DA 的延长线相 交于点 F．

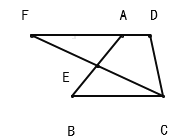
    （1）求证：△BCE≌△AFE；

    （2）连接 AC、FB，则 AC 与 FB 的数量关系是 ，位置关系是 ．

    查看答案和解析>>

    科目： 来源： 题型：

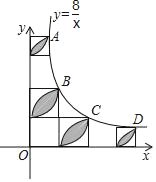
    【题目】已知，A、B、C、D是反比例函数y=（x＞0）图象上四个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形（如图）的边长为半径作四分之一圆周的两条弧，组成四个橄榄形（阴影部分），则这四个橄榄形的面积总和是__________（用含π的代数式表示）．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】(1)如图①，已知△ABC为直角三角形，∠A＝90°，若沿图中虚线剪去∠A，则∠1＋∠2等于(　　)

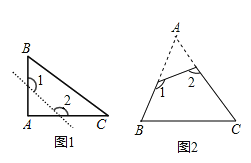
    A．90° B．135° C．270° D．315°

    (2)如图②，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1＋∠2＝________°；

    (3)根据(1)与(2)的求解过程，请你归纳猜想∠1＋∠2与∠A的关系是______________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标分别为（2，1），（6，1），∠BAC=90°，AB=AC，直线AB交y轴于点P，若△ABC与△A′B′C′关于点P成中心对称，则点A′的坐标为（　　）

    A. （﹣4，﹣5） B. （﹣5，﹣4） C. （﹣3，﹣4） D. （﹣4，﹣3）

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，BE，CE平分△ABC的两个外角，且交于点E，∠A＝80°.

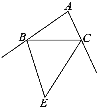
    (1)∠E的度数是多少？

    (2)若∠ABC＝35°，写出四边形ABEC各内角的度数．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，已知O是四边形ABCD内一点，OA＝OB＝OC，∠ABC＝∠ADC＝70°，则∠DAO＋∠DCO的大小是________．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（　　）

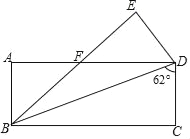
    A. 31° B. 28° C. 62° D. 56°

    查看答案和解析>>

    科目： 来源： 题型：

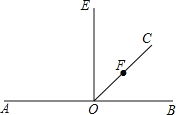
    【题目】如图，O为直线AB上一点，F为射线OC上一点，OE⊥AB．

    （1）用量角器和直角三角尺画∠AOC的平分线OD，画FG⊥OC，FG交AB于点G；

    （2）在（1）的条件下，比较OF与OG的大小，并说明理由；

    （3）在（1）的条件下，若∠BOC＝40°，求∠AOD与∠DOE的度数．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某商场计划购进A，B两种型号的手机，已知每部A型号手机的进价比每部B型号手机进价多500元，每部A型号手机的售价是2500元，每部B型号手机的售价是2100元．

    （1）若商场用50000元共购进A型号手机10部，B型号手机20部，求A、B两种型号的手机每部进价各是多少元？

    （2）为了满足市场需求，商场决定用不超过7.5万元采购A、B两种型号的手机共40部，且A型号手机的数量不少于B型号手机数量的2倍．

    ①该商场有哪几种进货方式？

    ②该商场选择哪种进货方式，获得的利润最大？

    查看答案和解析>>

    同步练习册答案