
科目: 来源: 题型:
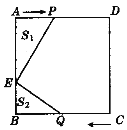
【题目】小英和小倩站在正方形的对角A,C两点处,小英以2米/秒的速度走向点D处,途中位置记为P,小倩以3米/秒的速度走向点B处,途中位置记为Q,假设两人同时出发,已知正方形的边长为8米,E在AB上,AE=6米,记三角形AEP的面积为S1平方米,三角形BEQ的面积为S2平方米,如图所示.
(1)她们出发后几秒时S1=S2;
(2)当S1+S2=15时,小倩距离点B处还有多远?
查看答案和解析>>
科目: 来源: 题型:
【题目】试根据图中信息,解答下列问题.

(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目: 来源: 题型:
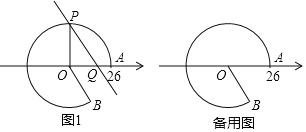
【题目】如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧![]() ,使点B在O右下方,且tan∠AOB=
,使点B在O右下方,且tan∠AOB=![]() ,在优弧
,在优弧![]() 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)若优弧上一段![]() 的长为13π,求∠AOP的度数及x的值;
的长为13π,求∠AOP的度数及x的值;
(2)求x的最小值,并指出此时直线l与![]() 所在圆的位置关系;
所在圆的位置关系;
(3)若线段PQ的长为12.5,直接写出这时x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米/秒的速度由点向点运动,同时点
厘米/秒的速度由点向点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.当一个点停止运动时,另一个点也随之停止运动.
点运动.当一个点停止运动时,另一个点也随之停止运动.

(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]() _______厘米;
_______厘米;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过
的运动速度相等,经过![]() 秒后,
秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,那么当点
的运动速度不相等,那么当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.

(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为响应党中央号召,决定针对沿江两种主要污染源:生活污水和沿江工厂污染物排放,分别用甲方案和乙方案进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值平均为0.3.第一年有40家工厂用乙方案治理.经过三年治理,境内沿江水质明显改善.
(1)第一年40家工厂用乙方案治理一年降低的Q值为______;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都有增加,第三年新增的用乙方案.新治理的工厂数量是第二年新增的用乙方案新治理的工厂数量的1.5倍,第三年用乙方案治理所降低的Q值为57,设第二年新增的用乙方案新治理的工厂数量为m家,第三年新增的用乙方案新治理的工厂数量为n家.
①请列出关于m、n的方程组,并求解;
②该市生活污水用甲方案治理,第一年降低的Q值为20.5,从第二年起,每年所降低的Q值比上一年都增加a.若第三年用甲乙两种方案治理所降低的Q值比第二年用甲乙两种方案治理所降低的Q值大32,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com