
科目: 来源: 题型:
【题目】阅读材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说
,也就是说![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离,这个结论可以推广为
对应的点之间的距离,这个结论可以推广为![]() 表示数轴上
表示数轴上![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:对于任何有理数![]() 是否有最小值?如果有,写出最小值;如果没有,请说明理由.
是否有最小值?如果有,写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于![]() ,问至少需取走多少个黄球?
,问至少需取走多少个黄球?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠B=∠C,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
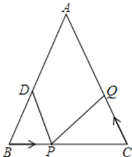
(1)用含t的式子表示PC的长为 ;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目: 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
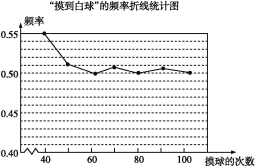
(1)请估计:当n足够大时,摸到白球的频率将会稳定在 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目: 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3;B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.若用(m,n)表示小明取球时m与n的对应值,则使关于x的一元二次方程x2-mx+![]() n=0有实数根的概率为__.
n=0有实数根的概率为__.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
①若∠A=70°,求∠BDC的度数.
②∠A=α,请用含有α的代数式表示∠BDC的度数.(直接写出答案)
(2)如图2,BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线.若∠A=α,请用含有α的代数式表示∠BEC的度数.
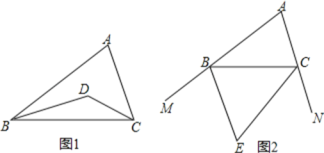
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com