
科目: 来源: 题型:
【题目】如图,△ABC中,AB=BC,BD⊥AC于点D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
∠ABC,且∠FAC在AC下方.点P,Q分别是射线BD,射线AF上的动点,且点P不与点B重合,点Q不与点A重合,连接CQ,过点P作PE⊥CQ于点E,连接DE.
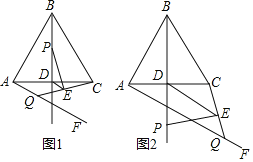
(1)若∠ABC=60°,BP=AQ.
①如图1,当点P在线段BD上运动时,请直接写出线段DE和线段AQ的数量关系和位置关系;
②如图2,当点P运动到线段BD的延长线上时,试判断①中的结论是否成立,并说明理由;
(2)若∠ABC=2α≠60°,请直接写出当线段BP和线段AQ满足什么数量关系时,能使(1)中①的结论仍然成立(用含α的三角函数表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
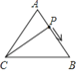
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目: 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目: 来源: 题型:
【题目】抚顺市某校想知道学生对“遥远的赫图阿拉”,“旗袍故里”等家乡旅游品牌的了解程度,随机抽取了部分学生进行问卷调查,问卷有四个选项(每位被调查的学生必选且只选一项)A.十分了解,B.了解较多,C.了解较少,D.不知道.将调查的结果绘制成如下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
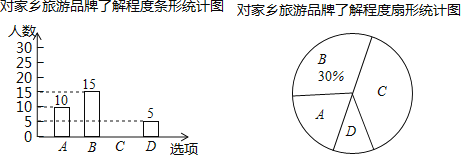
(1)本次调查了多少名学生?
(2)补全条形统计图;
(3)该校共有500名学生,请你估计“十分了解”的学生有多少名?
(4)在被调查“十分了解”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选两人做家乡旅游品牌宣传员,请用列表或画树状图法求出被选中的两人恰好是一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形AOBO2的顶点A的坐标为A(0,2),O1为正方形AOBO2的中心;以正方形AOBO2的对角线AB为边,在AB的右侧作正方形ABO3A1,O2为正方形ABO3A1的中心;再以正方形ABO3A1的对角线A1B为边,在A1B的右侧作正方形A1BB1O4,O3为正方形A1BB1O4的中心;再以正方形A1BB1O4的对角线A1B1为边在A1B1的右侧作正方形A1B1O5A2,O4为正方形A1B1O5A2的中心:…;按照此规律继续下去,则点O2018的坐标为_____.
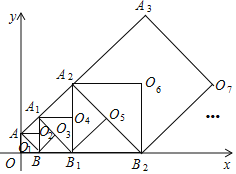
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法:
①在同一平面内,四条边相等的四边形一定是菱形。
②顺次连接矩形各边中点形成的四边形一定是正方形。
③对角线相等的四边形一定是矩形。
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分。
其中正确的有( )个.
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的取值范围.(温馨提示:如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达三边关系,a2+b2=c2)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com