
科目: 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:
+0.2 ,—0.2,+0. 7,—0.3,—0.4,+0.6,0,—0.1,—0.6,+0.5,—0.2,—0.5。
⑴求12箱苹果的总重量;
⑵若每箱苹果的重量标准为10![]() 0.5(千克),则这12箱有几箱不合乎标准的?
0.5(千克),则这12箱有几箱不合乎标准的?
查看答案和解析>>
科目: 来源: 题型:
【题目】若x满足(5-x)(x-2)=2,求(x-5)2+(2-x)2的值;
解:设5-x=a,x-2=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
所以(x-5)2+(2-x)2=(5-x)2+(x-2)2=a2+b2=(a+b)2-2ab=32-2×2=5,
请仿照上面的方法求解下面的问题
(1)若x满足(9-x)(x-4)=4,求(9-x)2+(x-4)2的值;
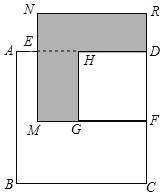
(2)已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且AE=2,CF=4,长方形EMFD的面积是63,分别以MF、DF为边作正方形,求阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a、b,那么![]() 的值为( ).
的值为( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A、B分别在y轴的正半轴和x轴的正半轴上,OA=OB,△AOB的面积为18.过点A作直线l⊥y轴.
(1)求点A的坐标;
(2)点C是第一象限直线l上一动点,连接BC,过点B作BD⊥BC,交y轴于点设点D的纵坐标为t,点C的横坐标为d,求t与d的关系式;
(3)在(2)的条件下,过点D作直线DF∥AB,交x轴于点F,交直线l于点E,OF=![]() EC时,求点E的坐标.
EC时,求点E的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出)
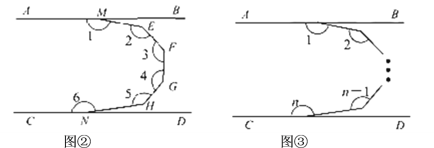
(1)如图①,已知 AB ∥CD,求证 :∠1+∠MEN+∠2=360°

(推广应用)
(2)如图②,已知 AB∥ CD,求∠1+∠2+∠3+∠4+∠5 +∠6的度数为___________.
如图③,已知 AB∥CD ,求∠1+∠2+∠3+∠4+∠5 +∠6+…+∠n的度数为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中,点D为BC的中点,BD=![]() AB,AD⊥BC.
AB,AD⊥BC.
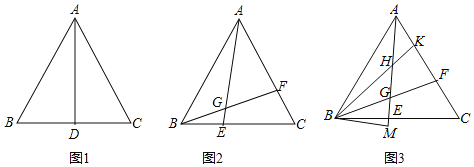
(1)如图1,求∠BAD的度数;
(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;
(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK=HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是斜边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:BD=AF;
(2)判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com