
科目: 来源: 题型:
【题目】已知:AD∥BC,点P为直线AB上一动点,点M在线段BC上,连接MP,![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点P在线段AB上时,若![]() ,
,![]() =150°,则
=150°,则![]() =________°;
=________°;
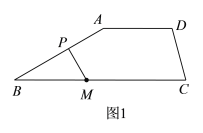
(2)如图2,当点P在AB的延长线上时,写出![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;

(3)如图3,当点P在BA的延长线上时,请画出图形,直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】数形结合是解决数学问题的重要思想方法,借助图形可以对很多数学问题进行直观推导和解释. 如图1,有足够多的A类、C类正方形卡片和B类长方形卡片. 用若干张A类、B类、C类卡片可以拼出如图2的长方形,通过计算面积可以解释因式分解:![]() .
.

(1)如图3,用1张A类正方形卡片、4张B类长方形卡片、3张C类正方形卡片,可以拼出以下长方形,根据它的面积来解释的因式分解为________;

(2)若解释因式分解![]() ,需取A类、B类、C类卡片若干张(三种卡片都要取到),拼成一个长方形,请画出相应的图形;
,需取A类、B类、C类卡片若干张(三种卡片都要取到),拼成一个长方形,请画出相应的图形;
(3)若取A类、B类、C类卡片若干张(三种卡片都要取到),拼成一个长方形,使其面积为![]() ,则m的值为________,将此多项式分解因式为________.
,则m的值为________,将此多项式分解因式为________.
查看答案和解析>>
科目: 来源: 题型:
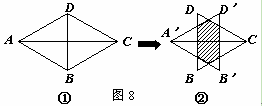
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________
查看答案和解析>>
科目: 来源: 题型:
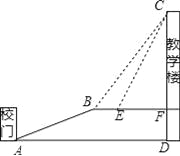
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i;(2)求DC的长.(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
查看答案和解析>>
科目: 来源: 题型:
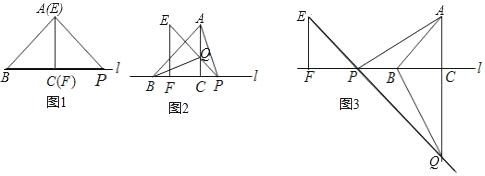
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“每周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
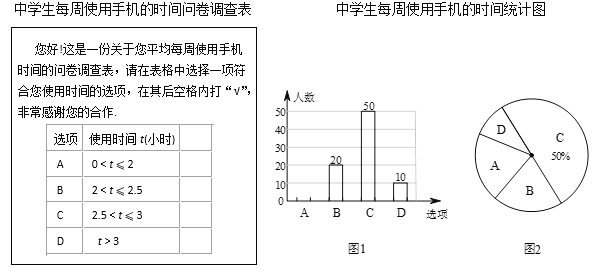
(1)本次接受问卷调查的共有________人;在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“A”选项的有多少名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com