
科目: 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A.∠A=∠C+∠E+∠FB.∠A+∠E-∠C-∠F=180°
C.∠A+∠C-∠E-∠F=180°D.∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目: 来源: 题型:
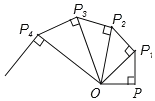
【题目】如图,OP=1,过P作PP1⊥OP,得OP1=![]() ;再过P1作P1P2⊥OP1且P1P2=1,得OP2=
;再过P1作P1P2⊥OP1且P1P2=1,得OP2=![]() ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,S1,S2,S3…分别表示各个三角形的面积,那么S12+S22+S32+…+S92的值是( )
;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,S1,S2,S3…分别表示各个三角形的面积,那么S12+S22+S32+…+S92的值是( )
A.![]() B.
B.![]() C.
C.![]() D.55
D.55
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
如图,在四边形 ABCD 中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,

求证:CD=AB
小刚是这样思考的;由已知可得,∠CAB=30°,∠DAC=75°,∠DCA=60°,∠ACB+∠DAC=180°,由求证及特殊度数可联想到构造特殊三角形,即过点 A 作 AE⊥AB 交 BC 的延长线于点 E,对 AB=AE,∠E=∠D
在△ADC 与△CEA 中,
∠D = ∠E,∠DAC = ∠ECA = 75° ,AC = CA.
△ADC≌△CEA.
得 CD=AE=AB
请你参考小刚同学思考问题的方法,解决下面问题
如图,在四边形 ABCD 中,若∠ACB+∠CAD=180°,∠B=∠D,请问:CD 与 AB 否相等?若相等,请你给出证明;若不相等。请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:平面直角坐标系中,把点A(m,4)(m是实数)向右移动7个单位向下移动2个单位得到点B,点B向左移动3个单位向上移动6个单位得到点C,请解答:
(1) 点B,C的坐标是:B ,C ;
(2) 求△ABC的面积;
(3)若连接OC交线段AB于点D,且△ACD与△BCD的面积比不超过0.75时,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
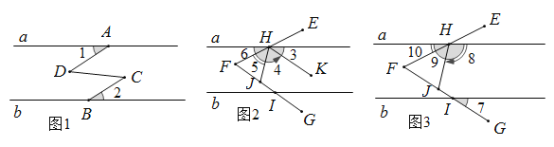
【题目】如图,A、B分别是直线a和b上的点,∠1=∠2,C、D在两条直线之间,且∠C=∠D.
(1) 证明:a∥b;
(2) 如图,∠EFG=60°,EF交a于H,FG交b于I,HK∥FG,若∠4=2∠3,判断∠5、∠6的数量关系,并说明理由;
(3) 如图∠EFG是平角的n分之1(n为大于1的整数),FE交a于H,FG交b于I.点J在FG上,连HJ.若∠8=n∠7,则∠9:∠10=______ .
查看答案和解析>>
科目: 来源: 题型:
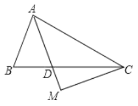
【题目】已知,如图,在△ABC 中,AD 平分∠BAC,AD=AB,CM⊥AD 于 M,请你通过观察和测量,猜想线段 AB、AC 之和与线段 AM 有怎样的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
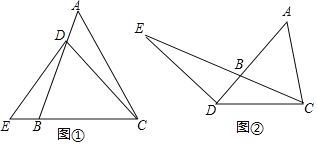
【题目】已知:![]() 是等腰三角形,其底边是BC,点D在直线AB上,E是直线BC上一点,且
是等腰三角形,其底边是BC,点D在直线AB上,E是直线BC上一点,且![]() .
.
![]() 如图
如图![]() ,点D在线段AB上,若
,点D在线段AB上,若![]() ,判断EB与AD的数量关系
,判断EB与AD的数量关系![]() 不必证明
不必证明![]() ;
;
![]() 若点D在线段AB的延长线上,其它条件不变
若点D在线段AB的延长线上,其它条件不变![]() 如图
如图![]() ,
,![]() 的结论是否成立,请说明理由;
的结论是否成立,请说明理由;
![]() 若
若![]() ,其它条件不变,EB与AD的数量关系是怎样的?
,其它条件不变,EB与AD的数量关系是怎样的?![]() 用含有
用含有![]() 的关系式直接写出结论,不要求写解答过程
的关系式直接写出结论,不要求写解答过程![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是一个运算流程.

(1)分别计算:当x=150时,输出值为 ,当x=17时,输出值为 ;
(2)若需要经过两次运算流程,才能运算输出y,求x的取值范围;
(3)请给出一个x的值,使之无论运算多少次都不能输出,并请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com