练习册

  • 练习册
  • 试题
    相关习题
     0  357089  357097  357103  357107  357113  357115  357119  357125  357127  357133  357139  357143  357145  357149  357155  357157  357163  357167  357169  357173  357175  357179  357181  357183  357184  357185  357187  357188  357189  357191  357193  357197  357199  357203  357205  357209  357215  357217  357223  357227  357229  357233  357239  357245  357247  357253  357257  357259  357265  357269  357275  357283  366461 

    科目： 来源： 题型：

    【题目】已知：如图，在Rt△ABC中，∠ACB=90°，AC=5，BC=12．在直线AC、BC上分别取一点M、N，使得△AMN≌△ABN，则CN=__________．

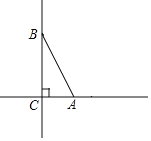
    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图1，，，满足：．．

    （1）______；

    （2）点是点左侧的轴上一点，连接，以为直角边作等腰直角，．连接，交于点；

    ①求．

    ②若平分，试求的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图所示，等边．

    （1）如图（1），若，现有两点、分别从点、点同时出发，沿三角形的边顺时针运动，已知点的速度为，点的速度为．当点第一次到达点时，、同时停止运动．点，运动______秒后，为等腰三角形．

    （2）如图，点位于等边的内部，且．将绕点顺时针旋转，点的对应点为点．

    ①依题意，补全图形；

    ②若，，求与的面积比．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知：如图，点是的边上的一点，过点作，，，为垂足，再过点作，交于点，且．

    （1）求证：；

    （2）求证：垂直平分．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，∠B=90°，AB=6cm，BC=12cm，动点P从点A开始沿边AB向B以1cm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以2cm/s的速度移动（不与点C重合）．如果P，Q分别从A，B同时出发，当四边形APQC的面积最小时，经过的时间为（ ）

    A. 1 s B. 2 s C. 3 s D. 4 s

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在某住房小区的建设中，为了提高业主的宜居环境，小区准备在一个长为米，宽为米的长方形草坪上修建两条宽为米的通道．

    （1）剩余草坪的面积是多少平方米？

    （2）当，时，剩余草坪的面积是多少平方米？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．如函数y=﹣x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时，恒有1≤y≤3，所以说函数y=﹣x+4是闭区间[1，3]上的“闭函数”，同理函数y=x也是闭区间[1，3]上的“闭函数”．

    （1）反比例函数y=是闭区间[1，2018]上的“闭函数”吗？请判断并说明理由；

    （2）如果已知二次函数y=x2﹣4x+k是闭区间[2，t]上的“闭函数”，求k和t的值；

    （3）如果（2）所述的二次函数的图象交y轴于C点，A为此二次函数图象的顶点，B为直线x=1上的一点，当△ABC为直角三角形时，写出点B的坐标．

    查看答案和解析>>

    科目： 来源： 题型：

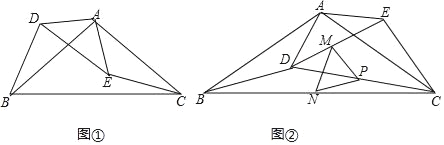
    【题目】如图①，在等腰△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE=120°．

    （1）求证：△ABD≌△ACE；

    （2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；

    （3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD=4，AB=6，请分别求出△PMN周长的最小值与最大值．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】2013年某企业按餐厨垃圾处理费25元/吨，建筑垃圾处理费16元/吨标准，共支付餐厨和建筑垃圾处理费5200元，从2014年元月起，收费标准上调为：餐厨垃圾处理费100元/吨，建筑垃圾处理费30元/吨，若该企业2014年处理的这两种垃圾数量与2013年相比没有变化，就要多支付垃圾处理费8800元，

    （1）该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨？

    （2）该企业计划2014年将上述两种垃圾处理量减少到240吨，且建筑垃圾处理费不超过餐厨垃圾处理量的3倍，则2014年该企业最少需要支付这两种垃圾处理费共多少元？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在直角坐标系中，先描出点，点.

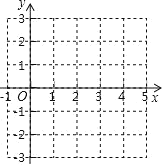
    （1）描出点关于轴的对称点的位置，写出的坐标 ；

    （2）用尺规在轴上找一点，使的值最小（保留作图痕迹）；

    （3）用尺规在轴上找一点，使（保留作图痕迹）.

    查看答案和解析>>

    同步练习册答案