
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上的一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E=![]() ;④S△ADE=7
;④S△ADE=7![]() .其中正确的是__________(写出所有正确结论的序号).
.其中正确的是__________(写出所有正确结论的序号).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ ABC 和△ADE都是等边三角形,点 B 在 ED 的延长线上.
(1)求证:△ABD≌△ACE.
(2)求证:AE+CE=BE.
(3)求∠BEC 的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目: 来源: 题型:
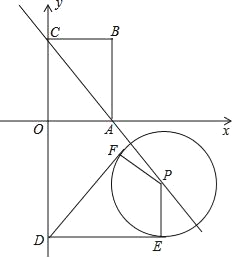
【题目】已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.
(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);
(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为![]() ,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.

查看答案和解析>>
科目: 来源: 题型:
【题目】箱子里有3个红球和2个黄球,从箱子中一次拿两个球出来.
(1)请你用列举法(树形图或列表)求一次拿出的两个球中时一红一黄的概率;
(2)往箱子中再加入x个白球,从箱子里一次拿出的两个球,多次实验统计如下
取出两个球的次数 | 20 | 30 | 50 | 100 | 150 | 200 | 400 |
至少有一个球是白球的次数 | 13 | 20 | 35 | 71 | 107 | 146 | 288 |
至少有一个球是白球的频率 | 0.65 | 0.67 | 0.70 | 0.71 | 0.713 | 0.73 | 0.72 |
请你估计至少有一个球是白球的概率是多少?
(3)在(2)的条件下求x的值.(![]() =0.7222222…)
=0.7222222…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com