
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
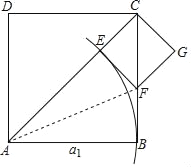
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
查看答案和解析>>
科目: 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.

(1)在图中画出![]() ,
,![]() 的面积是_____________;
的面积是_____________;
(2)若点![]() 与点
与点![]() 关于
关于![]() 轴对称,则点
轴对称,则点![]() 的坐标为_____________;
的坐标为_____________;
(3)已知![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数![]() 的图象于点A,交函数
的图象于点A,交函数![]() 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交![]() 于点C,边接AC.
于点C,边接AC.
(1)当点P的坐标为(1,0)时,求△ABC的面积;
(2)当点P的坐标为(1,0)时,在y轴上是否存在一点Q,使A、O、Q三点为顶点的三角形△QAO为等腰三角形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(3)请你连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com