【题目】（本题满分10分）一幢房屋的侧面外墙壁的形状如图所示，它由等腰三角形OCD和矩形ABCD组成，∠OCD=25°，外墙壁上用涂料涂成颜色相同的条纹，其中一块的形状是四边形EFGH，测得FG∥EH，GH=2.6m，∠FGB=65°。

【题目】为了解学生参加选课走板情况，学校研究小组随机抽取若干人进行调查分析，根据收集整理的数据绘制成不完整的条形统计图和扇形统计图，课程类别代码如下：

【题目】图1、图2分别是7×6的网格，网格中的每个小正方形的边长均为1，点A、B在小正方形的顶点上．

【题目】在△ABC中，∠ABC=60°，AD、CE分别平分∠BAC、∠ACB，

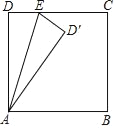
【题目】如图，矩形ABCD中，AD=10，AB=8，点E为边DC上一动点，连接AE，把△ADE沿AE折叠，使点D落在点D′处，当△DD′C是直角三角形时，DE的长为_____．

【题目】已知：如图，△ABC是等边三角形，延长AC到E，C为线段AE上的一动点（不与点A、E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ,OC. 以下五个结论：①AD=BE；②AP=BO；③PQ//AE；④∠AOB=60°；⑤OC平分∠AOE；结论正确的有_________（把你认为正确的序号都填上）

【题目】规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

【题目】如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：