
科目: 来源: 题型:
【题目】用无刻度的直尺绘图.
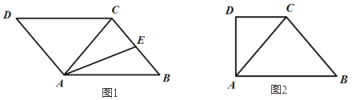
(1)如图1,在![]() 中,AC为对角线,AC=BC,AE是△ABC的中线.画出△ABC的高CH
中,AC为对角线,AC=BC,AE是△ABC的中线.画出△ABC的高CH
(2)如图2,在直角梯形![]() 中,
中,![]() ,AC为对角线,AC=BC,画出△ABC的高CH.
,AC为对角线,AC=BC,画出△ABC的高CH.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,ABCD中,∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目: 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源: 题型:
【题目】天水市某中学为了解学校艺术社团活动的开展情况,在全校范围内随机抽取了部分学生,在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,围绕你最喜欢哪一项活动(每人只限一项)进行了问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
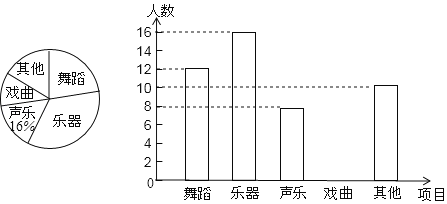
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生.
(2)请你补全条形统计图.
(3)扇形统计图中喜欢“乐器”部分扇形的圆心角为 度.
(4)请根据样本数据,估计该校1200名学生中喜欢“舞蹈”项目的共多少名学生?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料,解决问题
材料一:《孟子》中记载有一尺之棰,日取其半,万世不竭,其中蕴含了“有限”与“无限”的关系.如果我们要计算到第n天时,累积取走了多长的木棒?可以用下面两种方法去解决:
方法一:第n天,留下了![]() 尺木棒,那么累积取走了
尺木棒,那么累积取走了![]() 尺木棒.
尺木棒.
方法二:第1天取走了![]() 尺木棒,第2天取走了
尺木棒,第2天取走了![]() 尺木棒,……第n天取走了
尺木棒,……第n天取走了![]() 尺木棒,那么累积取走了:
尺木棒,那么累积取走了:![]() 尺木棒.
尺木棒.
设:![]() ……①
……①
由①×![]() 得:
得:![]() ……②
……②
①-②得:![]() 则:
则:![]()
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问题:1+2+3+…+100=?据说当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确的答案:(1+100)+(2+99)+…+(50+51)=101×50=5050.
也可以这样理解:令S=1+2+3+4+…+100 ①,则S=100+99+98+…+3+2+1②
①+②得:2S=(1+100)+(2+99)+(3+98)+…+(100+1)=100×(1+100)
即![]()
请用你学到的方法解决以下问题:
(1)计算:![]() ;
;
(2)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层的2倍,问塔的顶层共有多少盏灯?
(3)某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动,某一周,这款软件的激活码为下面数学问题的答案:已知一列数1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,……其中第1项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,以此类推,求满足如下条件的正整数N:
,以此类推,求满足如下条件的正整数N:![]() ,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com