[题目]在平面直角坐标系xOy中.抛物线y=x2﹣x+2m2+m(m＞0).与y轴交于点C.与x轴交于点A(x1.0).B(x2.0).且x1＜x2．(1)求2x1﹣x2+3的值,(2)当m=2x1﹣——青夏教育精英家教网—

相关习题

0 357647 357655 357661 357665 357671 357673 357677 357683 357685 357691 357697 357701 357703 357707 357713 357715 357721 357725 357727 357731 357733 357737 357739 357741 357742 357743 357745 357746 357747 357749 357751 357755 357757 357761 357763 357767 357773 357775 357781 357785 357787 357791 357797 357803 357805 357811 357815 357817 357823 357827 357833 357841 366461

科目： 来源： 题型：

【题目】在平面直角坐标系xOy中，抛物线y=x2﹣（3m+1）x+2m2+m（m＞0），与y轴交于点C，与x轴交于点A（x1，0），B（x2，0），且x1＜x2．

（1）求2x1﹣x2+3的值；

（2）当m=2x1﹣x2+3时，将此抛物线沿对称轴向上平移n个单位，使平移后得到的抛物线顶点落在△ABC的内部（不包括△ABC的边），求n的取值范围（直接写出答案即可）．

查看答案和解析>>

科目： 来源： 题型：

【题目】如果一个等腰三角形一条腰上的高等于另一腰的一半，则该等腰三角形的底角的度数_____．

查看答案和解析>>

科目： 来源： 题型：

【题目】如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．

（1）求证：四边形OCED是菱形；

（2）若∠BAC=30°，AC=4，求菱形OCED的面积．

查看答案和解析>>

科目： 来源： 题型：

【题目】如图，点P在∠MON的角平分线上，过点P作OP的垂线交OM，ON于C、D，PA⊥OM．PB⊥ON，垂足分别为A、B，EP∥BD，则下列结论错误的是（　　）

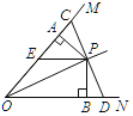
A.CP＝PDB.PA＝PBC.PE＝OED.OB＝CD

查看答案和解析>>

科目： 来源： 题型：

【题目】如图，已知AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE与CF交于点D，则下列结论中不正确的是（　　）

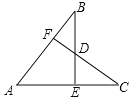
A. B. C. 点D在的平分线上D. 点D是CF的中点

查看答案和解析>>

科目： 来源： 题型：

【题目】某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动．顾客购买商品满200元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品；指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品．下表是该活动的一组统计数据：

转动转盘的次数n	100	150	200	500	800	1000
落在“一袋苹果”区域的次数m	68	108	140	355	560	690
落在“一袋苹果”区域的频率	0.68	0.72	0.70	0.71	0.70	0.69