
科目: 来源: 题型:
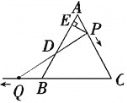
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线l的解析式为y=![]() x﹣1,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D(1,
x﹣1,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D(1,![]() )三点.
)三点.

(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;
(2)已知点 P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E,延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数,并求出S的最大值及S最大时点P的坐标;
(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知双曲线![]() (x>0),
(x>0),![]() (x>0),点P为双曲线
(x>0),点P为双曲线![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别交双曲线![]() 于D、C两点,则△PCD的面积为( )
于D、C两点,则△PCD的面积为( )

A. 1 B. ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:

![]() 求出样本容量,并补全直方图;
求出样本容量,并补全直方图;
![]() 该年级共有学生
该年级共有学生![]() 人,请估计全年级在这天里发言次数不少于
人,请估计全年级在这天里发言次数不少于![]() 次的人数;
次的人数;
![]() 已知
已知![]() 组发言的学生中恰有
组发言的学生中恰有![]() 位女生,
位女生,![]() 组发言的学生中恰有
组发言的学生中恰有![]() 位男生,现从
位男生,现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】初三学生小丽、小杰为了解本校初二学生每周上网的时间,各自在本校进行了抽样调查.小丽调查了初二电脑爱好者中![]() 名学生每周上网的时间,算得这些学生平均每周上网时间为
名学生每周上网的时间,算得这些学生平均每周上网时间为![]() 小时;小杰从全体
小时;小杰从全体![]() 名初二学生名单中随机抽取了
名初二学生名单中随机抽取了![]() 名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为
名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为![]() 小时.小丽与小杰整理各自样本数据,如下表所示.
小时.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周) | 小丽抽样人数 | 小杰抽样人数 |
|
|
|
|
|
|
|
|
|
|
|
|
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:

![]() 你认为哪位学生抽取的样本具有代表性?答:________;估计该校全体初二学生平均每周上网时间为________小时;
你认为哪位学生抽取的样本具有代表性?答:________;估计该校全体初二学生平均每周上网时间为________小时;
![]() 根据具有代表性的样本,把上图中的频数分布直方图补画完整;
根据具有代表性的样本,把上图中的频数分布直方图补画完整;
![]() 在具有代表性的样本中,中位数所在的时间段是________小时/周;
在具有代表性的样本中,中位数所在的时间段是________小时/周;
![]() 专家建议每周上网
专家建议每周上网![]() 小时以上(含
小时以上(含![]() 小时)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体初二学生中有多少名同学应适当减少上网的时间?
小时)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题.
例如:方程![]() 就可以这样来解:
就可以这样来解:
解:原方程可化为:![]()
所以![]() 或者
或者![]()
解方程![]() 得:
得:![]()
所以原方程的解:![]() ,
,![]()
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:![]() ;
;
(2)已知![]() 的三边为4、x、y,请你判断代数式
的三边为4、x、y,请你判断代数式![]() 的值的符号.
的值的符号.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足![]() .
.


(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC是等边三角形,点E、F分别为射线AC、射线CB上两点,CE=BF,直线EB、AF交于点D.
(1)当E、F在边AC、BC上时如图,求证:△ABF≌△BCE.

(2)当E在AC延长线上时,如图,AC=10,S△ABC=25![]() ,EG⊥BC于G,EH⊥AB于H,HE=8
,EG⊥BC于G,EH⊥AB于H,HE=8![]() ,EG= .
,EG= .

(3)E、F分别在AC、CB延长线上时,如图,BE上有一点P,CP=BD,∠CPB是锐角,求证:BP=AD.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了![]() 户家庭
户家庭![]() 年
年![]() 至
至![]() 月的用水量,统计得到的数据绘制成如图的两幅统计图,如图
月的用水量,统计得到的数据绘制成如图的两幅统计图,如图![]() 是这
是这![]() 户家庭总用水量的折线统计图,如图
户家庭总用水量的折线统计图,如图![]() 是这
是这![]() 户家庭月总用水量的不完整的条形统计
户家庭月总用水量的不完整的条形统计

![]() 根据图
根据图![]() 提供的信息,补全图
提供的信息,补全图![]() 中的条形统计图;
中的条形统计图;
![]() 求被抽查的
求被抽查的![]() 户家庭月总用水量的极差、众数、中位数;
户家庭月总用水量的极差、众数、中位数;
![]() 若该小区共有
若该小区共有![]() 户家庭,请你根据上述提供的统计数据,估计该住宅区
户家庭,请你根据上述提供的统计数据,估计该住宅区![]() 年的总用水量.
年的总用水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】九年级二班![]() 名同学在“爱心捐款”活动中,捐款情况统计如表,
名同学在“爱心捐款”活动中,捐款情况统计如表,
捐款金额(元) |
|
|
|
|
|
捐款人数(人) |
|
|
|
|
|
![]() 表中
表中![]() ________;
________;
![]() 二班同学捐款数组成的数据中,中位数是________、众数是________;
二班同学捐款数组成的数据中,中位数是________、众数是________;
![]() 九年级二班
九年级二班![]() 名同学平均捐款多少元?
名同学平均捐款多少元?
![]() 根据样本数据,估计该校九年级
根据样本数据,估计该校九年级![]() 名学生在本次活动中捐款多于
名学生在本次活动中捐款多于![]() 元的人数.
元的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com