
科目: 来源: 题型:
【题目】(1)已知![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,直线l经过点
,直线l经过点![]() ,分别从点
,分别从点![]() 、
、![]() 向直线l作垂线,垂足分别为
向直线l作垂线,垂足分别为![]() 、
、![]() .当点
.当点![]() ,
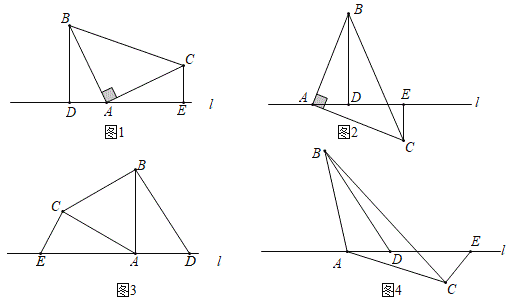
,![]() 位于直线l的同侧时(如图
位于直线l的同侧时(如图![]() ,易证
,易证![]() .如图2,若点
.如图2,若点![]() 在直线l的异侧,其它条件不变,
在直线l的异侧,其它条件不变,![]() 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.
(2)变式一:如图3,![]() 中,
中,![]() ,直线l经过点
,直线l经过点![]() ,点
,点![]() 、
、![]() 分别在直线l上,点
分别在直线l上,点![]() 、
、![]() 位于l的同一侧,如果
位于l的同一侧,如果![]() ,求证:
,求证:![]() .
.
(3)变式二:如图4,![]() 中,依然有
中,依然有![]() ,若点
,若点![]() ,
,![]() 位于l的两侧,如果
位于l的两侧,如果![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程,解应用题
甲乙两人相约周末到影院看电影,他们的家分别距离影院1200米和2000米,两人分别从家中同时出发,已知甲和乙的速度比是![]() ,结果甲比乙提前4分钟到达影院.
,结果甲比乙提前4分钟到达影院.
(1)求甲、乙两人的速度?
(2)在看电影时,甲突然接到家长电话让其15分钟内赶回家,时间紧迫改变速度,比来时每分钟多走25米,甲是否能按要求时间到家?
查看答案和解析>>
科目: 来源: 题型:
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险?请用你学过的知识加以解答.

查看答案和解析>>
科目: 来源: 题型:
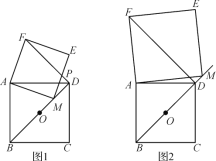
【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
查看答案和解析>>
科目: 来源: 题型:
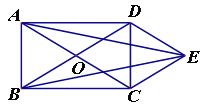
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班数学兴趣小组在学习二次根式时进行了如下题目的探索研究:
(1)填空![]() ;
;![]() ;
;
(2)观察第(1)题的计算结果回答:![]() 一定等于
一定等于
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .不确定
.不确定
(3)根据(1)、(2)的计算结果进行分析总结的规律,计算:![]() .
.
(4)请你参照数学兴趣小组的研究规律,化简:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100 m,200 m,1 000 m(分别用A1,A2,A3表示);田赛项目:跳远,跳高(分别用T1,T2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为_________;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率(请利用列表法或树状图加以说明).
查看答案和解析>>
科目: 来源: 题型:
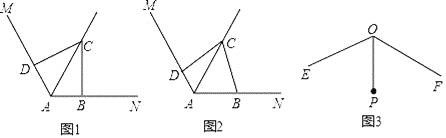
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com