
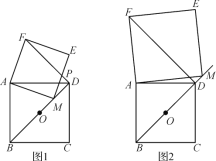
【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
【答案】(1)BM=DF,BM⊥DF.理由见解析;(2)BM=DF,BM⊥DF仍然成立,理由见解析.
【解析】
(1)根据图形,由正方形的性质证得△FAD≌△MAB,进而求出BM=DF,∠FDA=∠ABD=45°,结合已知条件即可推出BM=DF,BM⊥DF;
(2)成立,根据正方形的性质,推出△ABM≌△ADF,根据正方形的性质推出∠BAM=∠DAF,△ABM≌△ADF,进而求出BM=DF,∠ABM=∠ADF,∠BDF=∠ADB+∠ADF=90°即可.
(1)BM=DF,BM⊥DF.
理由:∵四边形ABCD,AMEF均为正方形,
∴AF=AM,AD=AB,∠FAM=∠DAB=90°,
∴∠FAM-∠DAM=∠DAB-∠DAM,即∠FAD=∠MAB.
在△FAD和△MAB中,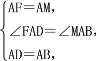
∴△FAD≌△MAB(SAS),∴BM=DF,∠FDA=∠ABD=45°.
∵∠ADB=45°,∴∠FDB=45°+45°=90°.∴BM⊥DF,即BM=DF,BM⊥DF.
(2)BM=DF,BM⊥DF仍然成立,
理由:∵四边形ABCD和AMEF均为正方形,∴AB=AD,AM=AF,∠BAD=∠MAF=90°,
∴∠FAM+∠DAM=∠DAB+∠DAM,即∠FAD=∠MAB.
在△FAD和△MAB中,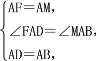
∴△FAD≌△MAB(SAS),∴BM=DF,∠ABM=∠ADF.
由正方形ABCD知,∠ABM=∠ADB=45°,
∴∠BDF=∠ADB+∠ADF=90°,即BM⊥DF.
∴(1)中的结论仍成立.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距d和身高h成如下所示的关系.

指距d(cm) | 20 | 21 | 22 | 23 |
身高h(cm) | 160 | 169 | 178 | 187 |
(1)直接写出身高h与指距d的函数关系式;
(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.

(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
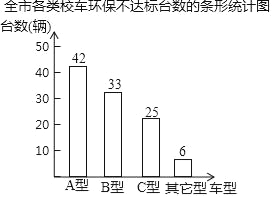
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出函数![]() 的图象,并利用图象回答问题:
的图象,并利用图象回答问题:
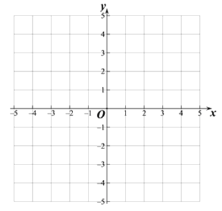
(1)写出图象与![]() 轴的交点A的坐标________,与
轴的交点A的坐标________,与![]() 轴的交点B的坐标________.
轴的交点B的坐标________.
(2)当![]() 时,
时,![]() 的取值范围是______________.
的取值范围是______________.
(3)有一点C的坐标是(3,4),顺次连接点A、B、C得到△ABC,三角形ABC的面积为________.
(4)点C关于![]() 轴对称的点D的坐标
轴对称的点D的坐标
(5)连接B,D两点,求直线BD的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com