
科目: 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,∠C>∠B,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)∠DAE与∠C-∠B有何关系?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ΔABC中,AD是高,AE、BF是角平分线,它们相交与点O,∠BAC=50°,∠C=70°,则∠DAC的度数为__________,∠BOA的度数为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目: 来源: 题型:
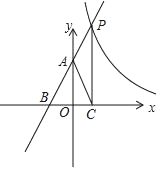
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
查看答案和解析>>
科目: 来源: 题型:
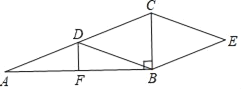
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
查看答案和解析>>
科目: 来源: 题型:
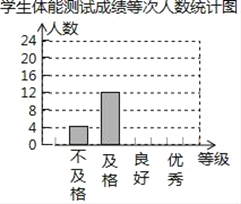
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中,正确的个数为( )
①三角形的三条高都在三角形内,且都相交于一点
②三角形的中线都是过三角形的某一个顶点,且平分对边的直线
③在△ABC中,若![]() ,则△ABC是直角三角形
,则△ABC是直角三角形
④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式x2+
,求代数式x2+![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() =4
=4
即![]() =4∴x+
=4∴x+![]() =4∴x2+
=4∴x2+![]() =(x+
=(x+![]() )2﹣2=16﹣2=14
)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
则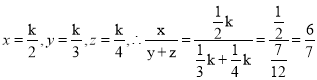
根据材料回答问题:
(1)已知![]() ,求x+
,求x+![]() 的值.
的值.
(2)已知![]() ,(abc≠0),求
,(abc≠0),求![]() 的值.
的值.
(3)若![]() ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
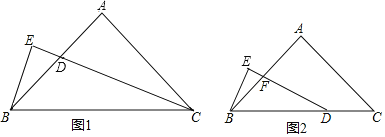
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com