
科目: 来源: 题型:
【题目】三个小岛![]() 、
、![]() 、
、![]() 的位置如图所示,在
的位置如图所示,在![]() 处测得小岛
处测得小岛![]() 在
在![]() 的北偏东
的北偏东![]() 方向,在
方向,在![]() 处测得小岛
处测得小岛![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且
方向,且![]() 、
、![]() 之间的距离是
之间的距离是![]() 海里,求:小岛
海里,求:小岛![]() 在小岛
在小岛![]() 的正东方向多少海里?(精确到
的正东方向多少海里?(精确到![]() 海里)(参考数据:
海里)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
查看答案和解析>>
科目: 来源: 题型:
【题目】(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:

(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
科目: 来源: 题型:
【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
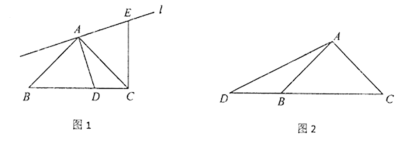
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等腰直角三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 的中点,点
的中点,点![]() 为斜边
为斜边![]() 所在直线上一动点,且三角形
所在直线上一动点,且三角形![]() 为等腰直角三角形(
为等腰直角三角形(![]() ,
,![]() 、
、![]() 、
、![]() 呈逆时针).
呈逆时针).
![]() 如图
如图![]() 点
点![]() 在边
在边![]() 上,判断
上,判断![]() 和
和![]() 的数量和位置关系,请直接写出你的结论.
的数量和位置关系,请直接写出你的结论.
![]() 如图
如图![]() 点
点![]() 在
在![]() 点左侧时;如图
点左侧时;如图![]() ,点
,点![]() 在
在![]() 点右侧.其他条件不变,
点右侧.其他条件不变,![]() 中结论是否仍然成立,并选择图
中结论是否仍然成立,并选择图![]() 或图
或图![]() 的一种情况来说明理由.
的一种情况来说明理由.
![]() 在图
在图![]() 中若
中若![]() ,连接
,连接![]() ,请猜测
,请猜测![]() 与
与![]() 的数量关系,即
的数量关系,即![]() ________
________![]() .(用含
.(用含![]() 的三角函数的式子表示)
的三角函数的式子表示)

查看答案和解析>>
科目: 来源: 题型:
【题目】一条船上午![]() 点在
点在![]() 处望见西南方向有一座灯塔
处望见西南方向有一座灯塔![]() (如图),此时测得船和灯塔相距
(如图),此时测得船和灯塔相距![]() 海里,船以每小时
海里,船以每小时![]() 海里的速度向南偏西
海里的速度向南偏西![]() 的方向航行到
的方向航行到![]() 处,这时望见灯塔在船的正北方向.(参考数据:
处,这时望见灯塔在船的正北方向.(参考数据:![]() ,
,![]() ).
).

![]() 求几点钟船到达
求几点钟船到达![]() 处;
处;
![]() 求船到达
求船到达![]() 处时与灯塔
处时与灯塔![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某海域有![]() 、
、![]() 、
、![]() 三艘船正在捕鱼作业,
三艘船正在捕鱼作业,![]() 船突然出现故障,向
船突然出现故障,向![]() 、
、![]() 两船发出紧急求救信号,此时
两船发出紧急求救信号,此时![]() 船位于
船位于![]() 船的北偏西
船的北偏西![]() 方向,距
方向,距![]() 船
船![]() 海里的海域,
海里的海域,![]() 船位于
船位于![]() 船的北偏东
船的北偏东![]() 方向,同时又位于
方向,同时又位于![]() 船的北偏东
船的北偏东![]() 方向.
方向.

(1)求![]() 的度数;
的度数;
![]() 船以每小时
船以每小时![]() 海里的速度前去救援,问多长时间能到出事地点.(结果精确到
海里的速度前去救援,问多长时间能到出事地点.(结果精确到![]() 小时).(参考数据:
小时).(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在水上治安指挥塔![]() 西侧两条航线
西侧两条航线![]() 、
、![]() 上有两艘巡逻艇
上有两艘巡逻艇![]() 与
与![]() 所在航线靠近
所在航线靠近![]() ,直线
,直线![]() 、
、![]() 间的距离
间的距离![]() ,点
,点![]() 在点
在点![]() 的南偏西
的南偏西![]() 方向上,且
方向上,且![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向上.求:
方向上.求:

![]() 巡逻艇
巡逻艇![]() 与塔
与塔![]() 之间的距离
之间的距离![]() .(结果保留根号)
.(结果保留根号)
![]() 已知巡逻艇
已知巡逻艇![]() 的速度每小时比巡逻艇
的速度每小时比巡逻艇![]() 快
快![]() ,当两艘巡逻艇同时到达指挥塔
,当两艘巡逻艇同时到达指挥塔![]() 的正南方向时,求巡逻艇
的正南方向时,求巡逻艇![]() 的速度.
的速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的直角边
的直角边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第象限,将
在第象限,将![]() 绕点
绕点![]() 按逆时针方向旋转至
按逆时针方向旋转至![]() ,使点
,使点![]() 的对应点
的对应点![]() 落在
落在![]() 轴的正半轴上,已知
轴的正半轴上,已知![]() ,
,![]() .
.

![]() 求点
求点![]() 和点
和点![]() 的坐标;
的坐标;
![]() 求经过点
求经过点![]() 和点
和点![]() 的直线所对应的一次函数解析式,并判断点
的直线所对应的一次函数解析式,并判断点![]() 是否在直线
是否在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com