
科目: 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶![]() 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④![]() <0,其中正确的结论是_____.
<0,其中正确的结论是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,则HG+HC的最小值为______________.
,点H是BD上的一个动点,则HG+HC的最小值为______________.

查看答案和解析>>
科目: 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“![]() ”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如将多项式
”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如将多项式![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,![]() ,此时可以得到数字密码
,此时可以得到数字密码![]() 或
或![]() 等.
等.
(1)根据上述方法,当![]() ,
,![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码(写出四个即可)?
分解因式后可以形成哪些数字密码(写出四个即可)?
(2)将多项式![]() 因式分解成三个一次式的乘积后,利用题目中所示的方法,当
因式分解成三个一次式的乘积后,利用题目中所示的方法,当![]() 时可以得到密码
时可以得到密码![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
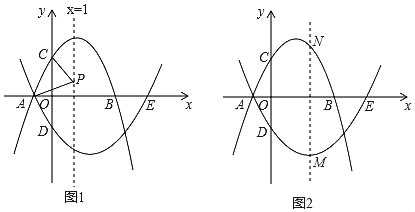
【题目】如图1,抛物线l1:y=﹣x2+bx+3交x轴于点A、B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣5).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA、PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴(如图2所示),交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.

(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=![]() ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DFGF.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.

(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
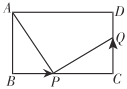
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒,且
秒,且![]() .
.

(1)![]() _________
_________![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)如图,当点![]() 从点
从点![]() 开始运动的同时,点
开始运动的同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得以
值,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与以
为顶点的三角形与以![]() 、
、![]() 、
、![]() 为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
为顶点的三角形全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com