
科目: 来源: 题型:
【题目】我们知道,演绎推理的过程称为证明,证明的出发点和依据是基本事实.证明三角形全等的基本事实有:两边及其夹角分别相等的两个三角形全等,两角及其夹边分别相等的两个三角形全等,三边分别相等的两个三角形全等.
(1)请选择利用以上基本事实和三角形内角和定理,结合下列图形,证明:两角分别相等且其中一组等角的对边相等的两个三角形全等.

(2)把三角形的三条边和三个角统称为三角形的六个元素.如果两个三角形有四对对应元素相等,这两个三角形一定全等吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() (
(![]() ,
,![]() 是常数,
是常数,![]() )的图象过
)的图象过![]() ,
,![]() 两点.
两点.
(1)在图中画出该一次函数并求其表达式;

(2)若点![]() 在该一次函数图象上,求
在该一次函数图象上,求![]() 的值;
的值;
(3)把![]() 的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图形,并直接写出新函数图象对应的表达式.
的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图形,并直接写出新函数图象对应的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据:
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(写两条支持你结论的理由).
查看答案和解析>>
科目: 来源: 题型:
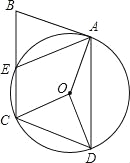
【题目】如图,ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.
(1)求证:AB=AE;
(2)试探究α与β之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
(2)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料,并解决问题.
(1)已知在△ABC中,∠A=60°,图1-图3的△ABC的内角平分线或外角平分线交于点O,请直接求出下列角度的度数.


如图1,∠O= ; 如图2,∠O= ; 如图3,∠O= ;如图4,∠ABC,∠ACB的三等分线交于点O1,O2,连接O1O2,则∠BO2O1= .
(2)如图5,点O是△ABC两条内角平分线的交点,求证:∠O=90°+![]() ∠A.
∠A.
(3)如图6,△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1,O2,若∠1=115°,∠2=135°,求∠A的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠ACB=900,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ并延长交AC于点F,试证明:FC(AC+BC)为定值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com