【题目】如图，一条抛物线与轴相交于、两点，其顶点在折线上移动，若点、、的坐标分别为、、，点的横坐标的最小值为，则点的横坐标的最大值为（ ）

A. 1 B. 2 C. 3 D. 4

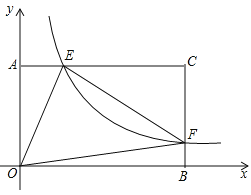
【题目】在矩形AOBC中，OB=6，OA=4，分别以OB，OA所在直线为x轴和y轴建立如图所示的平面直角坐标系，F是BC上的一个动点（不与B、C重合），过F点的反比例函数（k＞0）的图象与AC边交于点E，连接OE，OF，EF．

（1）若tan∠BOF=，求F点的坐标；

（2）当点F在BC上移动时，△OEF与△ECF的面积差记为S，求当k为何值时，S有最大值，最大值是多少？

（3）是否存在这样的点F，使得△OEF为直角三角形？若存在，求出此时点F坐标；若不存在，请说明理由。

【题目】“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数的图象交于点P，以P为圆心、以2OP为半径作弧交图象于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=∠AOB．要明白帕普斯的方法，请研究以下问题：

（1）设P（，）、R（，），求直线OM对应的函数表达式（用含，的代数式表示）；

（2）分别过点P和R作y轴和x轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB=∠AOB；

（3）应用上述方法得到的结论，你如何三等分一个钝角（用文字简要说明）

（1）如图1，直接写出∠ADB的度数　 　；

（2）如图2，作∠ABM=60°在BM上截取BE，使BE=BA，连接CE，判断CE与AD的数量关系，请补全图形，并加以证明；

（3）在（2）的条件下，连接DE，AE．若∠DEC=60°，DE=2，求AE的长．

例题：若, 求m和n的值

解：∵

∴

∴

∴，

∴，

问题：(1)若，求的值．

(2)已知a，b，c是△ABC的三边长，满足,且c是△ABC中最长的边，求c的取值范围．

（1）如图甲，边长为a的大正方形中有一个边长为b的小正方形，请你写出阴影部分面积是 （写成两数平方差的形式）

（2）小颖将阴影部分裁下来，重新拼成一个长方形，如图乙，则长方形的长是 ，宽是 ，面积是 （写成多项式乘法的形式）．

（3）比较甲乙两图阴影部分的面积，可以得到公式 （用式子表达）

（4）运用你所得到的公式计算：10.3×9.7．

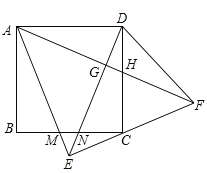
【题目】如图，正方形ABCD中，以AD为底边作等腰△ADE，将△ADE沿DE折叠，点A落到点F处，连接EF刚好经过点C，再连接AF，分别交DE于点G，交CD于点H，下列结论：①△ABM≌△DCN；②∠DAF=30°；③△AEF是等腰直角三角形；④EC=CF；⑤，其中正确的有__________.

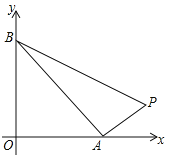
【题目】如图，由点P（14,1），A（，0），B（0，）（），确定的△PAB的面积为18，则的值为_________，如果，则的值为_____________________

（1）猜想△ABC的形状　 　，并证明；

（2）直接写出△ABC的面积=　 　；

（3）画出△ABC关于直线l的轴对称图形△A1B1C1．