
科目: 来源: 题型:
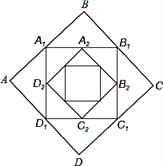
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在平面直角坐标系中,点![]() ,点
,点![]() 是
是![]() 轴上方的点,且
轴上方的点,且![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.

(1)当![]() 时,求
时,求![]() 的长.
的长.
(2)求证:![]() .
.
(3)若![]() 的中点为
的中点为![]() ,探究点
,探究点![]() 横坐标的规律.
横坐标的规律.
特殊情况探究:①当![]() 时,求出此时点
时,求出此时点![]() 的横坐标为6,②当
的横坐标为6,②当![]() 时,求得此时点
时,求得此时点![]() 的横坐标为______.
的横坐标为______.
一般情况探究:③当![]() 时,点
时,点![]() 横坐标的规律是什么?并证明这个规律.
横坐标的规律是什么?并证明这个规律.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是三种电话计费方式:
月使用费 (元) | 主叫限定时间 (分钟) | 主叫超时收费 (元/分钟) | 被叫 | |
方式一 | 18 | 60 | 0.2 | 免费 |
方式二 | 28 | 120 | 0.2 | 免费 |
方式三 | 48 | 240 | 0.2 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费.
设一个月内主叫通话![]() 分钟(
分钟(![]() 为正整数).
为正整数).
(1)当![]() 时,按方式一计费为______元;按方式二计费为______元.
时,按方式一计费为______元;按方式二计费为______元.
(2)当![]() 时,是否存在某一时间
时,是否存在某一时间![]() ,使方式二与方式三的计费结果相等?若存在,请求出对应的值,若不存在,请说明理由.
,使方式二与方式三的计费结果相等?若存在,请求出对应的值,若不存在,请说明理由.
(3)当![]() 时,哪一种收费方式最省钱?请说明理由.
时,哪一种收费方式最省钱?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
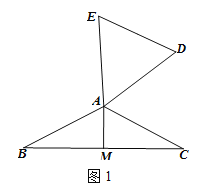
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
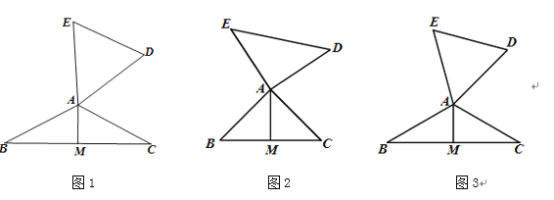
(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。
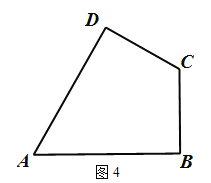
(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。
查看答案和解析>>
科目: 来源: 题型:
【题目】下列五个命题:![]() 两个端点能够重合的弧是等弧;
两个端点能够重合的弧是等弧;![]() 圆的任意一条弧必定把圆分成劣弧和优弧两部分
圆的任意一条弧必定把圆分成劣弧和优弧两部分![]() 经过平面上任意三点可作一个圆;
经过平面上任意三点可作一个圆;![]() 任意一个圆有且只有一个内接三角形
任意一个圆有且只有一个内接三角形![]() 三角形的外心到各顶点距离相等.其中真命题有( )
三角形的外心到各顶点距离相等.其中真命题有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,并连结CN.求证:AB=CN+CM.
(2)(类比探究)如图2,在等边△ABC中,若点M是BC延长线上的任意一点(不含端点C),其它条件不变,则AB=CN+CM是否还成立?若成立,请说明理由;若不成立,请写出AB,CN,CM三者之间的数量关系,并给予证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,以
,以![]() 为直径作
为直径作![]() D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
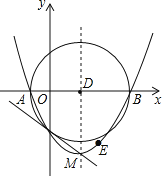
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
,![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙O 的半径是![]() ,
,
①求出⊙O上的所有梦之点的坐标;
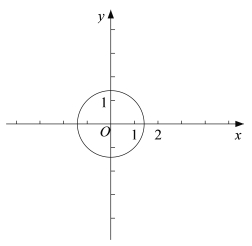
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com