
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,以
,以![]() 为直径作
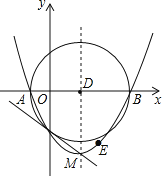
为直径作![]() D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
①根据抛物线的解析式得出抛物线与x轴的交点A、B坐标,由抛物线的对称性即可判定;②求得⊙D的直径AB的长,得出其半径,由圆的面积公式即可判定,③过点C作CE∥AB,交抛物线于E,如果CE=AD,则根据一组对边平行且相等的四边形是平行四边形即可判定;④求得直线CM、直线CD的解析式通过它们的斜率进行判定.
∵在y=![]() (x+2)(x-8)中,当y=0时,x=-2或x=8,
(x+2)(x-8)中,当y=0时,x=-2或x=8,
∴点A(-2,0)、B(8,0),
∴抛物线的对称轴为x=![]() =3,故①正确;
=3,故①正确;
∵⊙D的直径为8-(-2)=10,即半径为5,
∴⊙D的面积为25π,故②错误;
在y=![]() (x+2)(x-8)=
(x+2)(x-8)=![]() x2-
x2-![]() x-4中,当x=0时y=-4,
x-4中,当x=0时y=-4,
∴点C(0,-4),
当y=-4时,![]() x2-
x2-![]() x-4=-4,
x-4=-4,
解得:x1=0、x2=6,
所以点E(6,-4),
则CE=6,
∵AD=3-(-2)=5,
∴AD≠CE,
∴四边形ACED不是平行四边形,故③错误;
∵y=![]() x2-
x2-![]() x-4=
x-4=![]() (x-3)2-
(x-3)2-![]() ,
,
∴点M(3,-![]() ),
),
设直线CM解析式为y=kx+b,
将点C(0,-4)、M(3,-![]() )代入,
)代入,
得: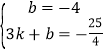 ,
,
解得: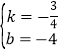 ,
,
所以直线CM解析式为y=-![]() x-4;
x-4;
设直线CD解析式为y=mx+n,
将点C(0,-4)、D(3,0)代入,得:![]() ,
,
解得: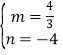 ,
,
所以直线CD解析式为y=![]() x-4,
x-4,
由-![]() ×
×![]() =-1知CM⊥CD于点C,
=-1知CM⊥CD于点C,
∴直线CM与⊙D相切,故④正确;
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,PB切⊙O于点B,PO交⊙O于点E,延长PO交⊙O于点A,连结AB,⊙O的半径OD⊥AB于点C,BP=6,∠P=30°,则CD的长度是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“还城市一片蓝天”,市政府决定大力发展公共交通,鼓励市民乘公交车或地铁出行.设每天公交车和地铁的运营收入为y百万元,客流量为x百万人,以(x,y)为坐标的点都在左图中对应的射线上.其中,运营收入=票价收入﹣运营成本.交通部门经过调研,采取了如图所示的调整方案.

(1)在左图中,代表公交车运营情况的(x,y)对应的点在射线 上,公交车的日运营成本是 百万元,当客流量x满足 时,公交车的运营收入超过4百万元;
(2)求调整后地铁每天的运营收入和客流量之间的函数关系,不要求写自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B(m,﹣2).
的图象交于点A(1,4)和点B(m,﹣2).

(1)求一次函数的关系式;
(2)求△AOB的面积;
(3)观察图象,写出使得y1≤y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(多选)在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离
地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系,下列说法正确的是( )
(小时)的函数关系,下列说法正确的是( )

A.甲乙两车出发2小时后相遇
B.甲车速度是40千米/小时
C.相遇时乙车距离![]() 地100千米
地100千米
D.乙车到![]() 地比甲车到
地比甲车到![]() 地早
地早![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com