
科目: 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目: 来源: 题型:
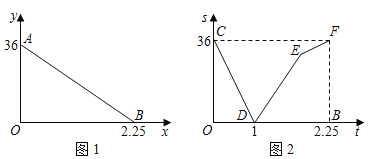
【题目】小明从家出发沿一条笔直的公路骑自行车前往图书馆看书,他与图书馆之间的距离y(km)与出发时间t(h)之间的函数关系如图1中线段AB所示,在小明出发的同时,小明的妈妈从图书馆借书结束,沿同一条公路骑电动车匀速回家,两人之间的距离s(km)与出发时间t(h)之间的函数关系式如图2中折线段CD﹣DE﹣EF所示.
(1)小明骑自行车的速度为 km/h、妈妈骑电动车的速度为 km/h;
(2)解释图中点E的实际意义,并求出点E的坐标;
(3)求当t为多少时,两车之间的距离为18km.
查看答案和解析>>
科目: 来源: 题型:
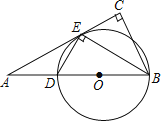
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目: 来源: 题型:
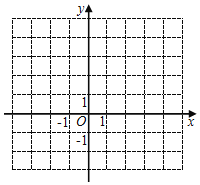
【题目】已知:A(1,0),B(0,4),C(4,2).
(1)在坐标系中描出各点(小正方形网格的长度为单位1),画出△ABC;(三点及连线请加黑描重)
(2)若△A1B1C1与△ABC关于y轴对称,请在图中画出△A1B1C1;
(3)点Q是x轴上的一动点,则使QB+QC最小的点Q坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)

查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
查看答案和解析>>
科目: 来源: 题型:
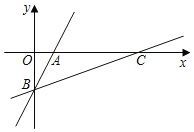
【题目】如图,在平面直角坐标系中,一次函数y=2x﹣4的图象分別交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com