
科目: 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,过C作AB边上的高CD,H为BC边上的中点,连接DH,CD上有一点F,且AD=DF,连接BF并延长交AC于E,交DH于G.
(1)若AC=5,DH=2,求DF的长.
(2)若AB=CB,求证:BG=![]() AE.
AE.

查看答案和解析>>
科目: 来源: 题型:
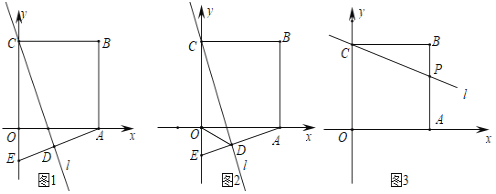
【题目】如图,正方形OABC的顶点O是坐标原点,边OA和OC分别在x轴、y轴上,点B的坐标为(4,4).直线l经过点C.
(1)若直线l与边OA交于点M,过点A作直线l的垂线,垂足为D,交y轴于点E.
①如图1,当OE=1时,求直线l对应的函数表达式;
②如图2,连接OD,求证:OD平分∠CDE.
(2)如图3,若直线l与边AB交于点P,且S△BCP=![]() S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD中,AB=6cm,∠ADC=60°,点E从点D出发,以1cm/s的速度沿射线DA运动,同时点F从点A出发,以1cm/s的速度沿射线AB运动,连接CE、CF和EF,设运动时间为t(s).
(1)当t=3s时,连接AC与EF交于点G,如图①所示,则EF= cm;
(2)当E、F分别在线段AD和AB上时,如图②所示,
①求证:△CEF是等边三角形;
②连接BD交CE于点G,若BG=BC,求EF的长和此时的t值.
(3)当E、F分别运动到DA和AB的延长线上时,如图③所示,若EF=3![]() cm,直接写出此时t的值.
cm,直接写出此时t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】小王同学准备筹集资金为贫困山区儿童捐款,打算从淘宝网上购进一批闪光发箍和荧光棒在某演唱会现场出售,其中闪光发箍的购买价格为6元/个,荧光棒的购买价格为8元/个.
(1)小王计划购进闪光发箍和荧光棒共120个,且将闪光发箍加价40%、荧光棒加价20%后出售.当所有物品售完后,若利润不低于256元,则小王至少应购买闪光发箍多少个?
(2)小王调整了方案,决定将闪光发箍的售价在进价的基础上上涨(a+10)%、荧光棒的售价在进价基础上上涨a%,在(1)中闪光发箍购买量取得最小值的情况下,将闪光发箍的购买量提![]() a%,而荧光棒的购买量保持不变,则全部售出后,最终可获利246.4元,请求出a的值.
a%,而荧光棒的购买量保持不变,则全部售出后,最终可获利246.4元,请求出a的值.
查看答案和解析>>
科目: 来源: 题型:
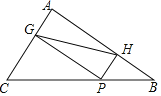
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
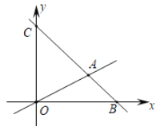
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.
查看答案和解析>>
科目: 来源: 题型:
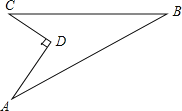
【题目】如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=ax+b(a≠0)与y轴交与点C,与双曲线y=![]() (m≠0)交于A、B两点,AD⊥y轴于点D,连接BD,已知OC=AD=2,cos∠ACD=
(m≠0)交于A、B两点,AD⊥y轴于点D,连接BD,已知OC=AD=2,cos∠ACD=![]() .
.
(1)求直线AB和双曲线的解析式.
(2)求△ABD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com