
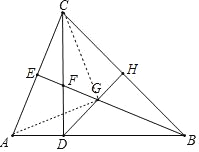
【题目】如图,△ABC中,∠ABC=45°,过C作AB边上的高CD,H为BC边上的中点,连接DH,CD上有一点F,且AD=DF,连接BF并延长交AC于E,交DH于G.
(1)若AC=5,DH=2,求DF的长.
(2)若AB=CB,求证:BG=![]() AE.
AE.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)只要证明△ADC≌△FDB(SAS),即可推出BF=AC=5,再利用勾股定理即可解决问题;
(2)如图,连接CG,AG.想办法证明GA=GB=GC,△AEG是等腰直角三角形即可解决问题.
(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
∵∠ABC=45°,
∴DC=DB,
∵AD=DF,
∴△ADC≌△FDB(SAS),
∴BF=AC=5,
∵CH=HB,
∴BC=2DH=4,
∴BD=DC=2![]() ,
,
在Rt△DFB中,DF=![]() =
=![]() =
=![]() .
.
(2)如图,连接CG,AG.
∵△ADC≌△FDB,
∴∠ACD=∠FBD,
∵∠CFE=∠BFD,
∴∠CEF=∠FDB=90°,
∴∠CEF=90°,
∴BE⊥AC,
∵BA=BC,
∴AE=EC,
∴GC=GA,
∵GH⊥BC,HC=HB,
∴GC=GB,
∴GB=AG,
∵∠ABG=∠CBG=22.5°,
∴∠GCB=∠GBC=22.5°,∠GAB=∠GBA=22.5°,
∴∠CGE=45°,∠AEG=45°,
∴△AEG是等腰直角三角形,
∴AG=BG=![]() AE.
AE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①△DFP~△BPH;②![]() ;③PD2=PHCD;④
;③PD2=PHCD;④![]() ,其中正确的是______(写出所有正确结论的序号).
,其中正确的是______(写出所有正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
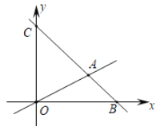
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=![]() x2+
x2+![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧)与y轴交于点C,直线BE⊥BC与点B,与抛物线的另一交点为E.
与x轴交于A、B两点(点A在点B的左侧)与y轴交于点C,直线BE⊥BC与点B,与抛物线的另一交点为E.
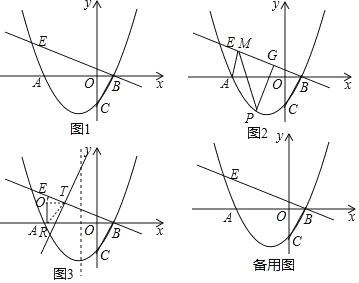
(1)如图1,求点E的坐标;
(2)如图2,若点P为x轴下方抛物线上一动点,过P作PG⊥BE与点G,当PG长度最大时,在直线BE上找一点M,使得△APM的周长最小,并求出周长的最小值.
(3)如图3,将△BOC在射线BE上,设平移后的三角形为△B′O′C′,B′在射线BE上,若直线B′C′分别与x轴、抛物线的对称轴交于点R、T,当△O′RT为等腰三角形时,求R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
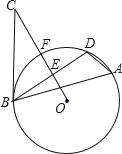
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com