
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
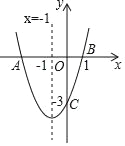
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
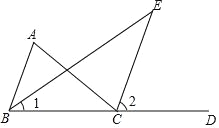
【题目】如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E,以下是小明的证明过程,请在括号里填写理由.
证明:∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知)
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(_________)
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知)
∴∠ACD=2∠2,∠ABC=2∠1(_______)
∴∠A=2∠2﹣2∠1(_________)
=2(∠2﹣∠1)(_________)
=2∠E(等量代换)
(2)如果∠A=∠ABC,求证:CE∥AB.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在平面直角坐标系中A(3,2),B(4,3),C(1,1).
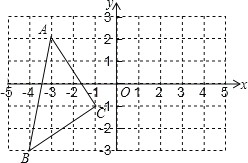
(1)在图中作出△ABC关于y轴对称图形△A1B1C1;
(2)写出A1、B1、C1的坐标分别是A1(___,___),B1(___,___),C1(___,___);
(3)△ABC的面积是___.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
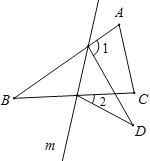
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
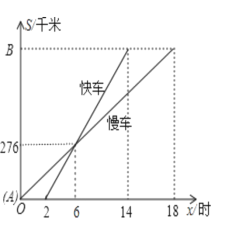
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目: 来源: 题型:
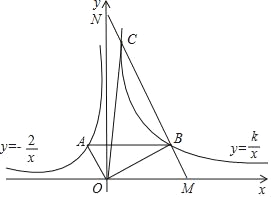
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com