
科目: 来源: 题型:
【题目】利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
(1)如图①,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
(2)如图②,在平面直角坐标系中,![]() 为等腰直角三角形,直角顶点
为等腰直角三角形,直角顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
(3)如图③,![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .则
.则![]() .(只需写出结果,用含
.(只需写出结果,用含![]() ,
,![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=![]() 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
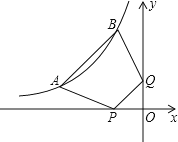
A.y=x B.y=x+1 C.y=x+2 D.y=x+3
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+x+c的顶点坐标为(1,-4),图象又经过点(2,-3).
求:(1)抛物线y=ax2+x+c的解析式.
(2)求抛物线y=ax2+x+c与一次函数y=3x+11的交点坐标.
(3)求不等式ax2+x+c>3x+11的解集(直接写出答案).
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车分别从![]() ,
,![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地.甲、乙两车距B地的路程
地.甲、乙两车距B地的路程![]() (
(![]() )与各自行驶的时间
)与各自行驶的时间![]() (
(![]() )之间的关系如图所示.
)之间的关系如图所示.
(1)求甲车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当甲车到达![]() 地时,乙车距
地时,乙车距![]() 地的路程为
地的路程为 ![]()

查看答案和解析>>
科目: 来源: 题型:
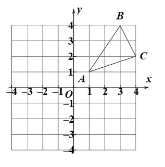
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)在图中画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)通过平移,使![]() 移动到原点
移动到原点![]() 的位置,画出平移后的
的位置,画出平移后的![]() .
.
(3)在![]() 中有一点
中有一点![]() ,则经过以上两次变换后点
,则经过以上两次变换后点![]() 的对应点
的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

查看答案和解析>>
科目: 来源: 题型:
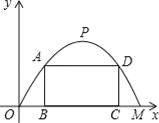
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
查看答案和解析>>
科目: 来源: 题型:
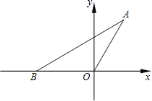
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积是
的面积是![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 求过点
求过点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
![]() 在
在![]() 中抛物线的对称轴上是否存在点
中抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 在
在![]() 中
中![]() 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,线段
,线段![]() 把
把![]() 分成两个三角形,使其中一个三角形面积与四边形
分成两个三角形,使其中一个三角形面积与四边形![]() 面积比为
面积比为![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
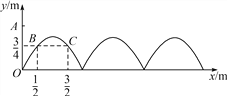
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com