
科目: 来源: 题型:
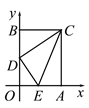
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
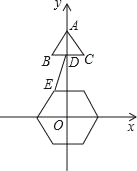
【题目】如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A. 3 B. 4﹣![]() C. 4 D. 6﹣2
C. 4 D. 6﹣2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:如图1,![]() 中,点
中,点![]() ,
,![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
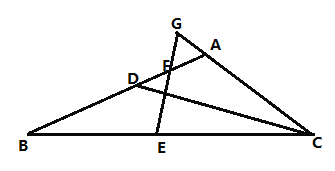
等腰三角形是一种常见的轴对称图形,几何试题中我们常将一腰所在的三角形沿着等腰三角形的对称轴进行翻折,从而构造轴对称图形.
①小明的想法是:将![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的对称轴进行翻折,即作
的对称轴进行翻折,即作![]() 交
交![]() 于
于![]() (如图2)
(如图2)
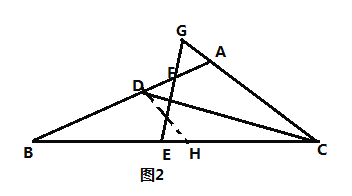
②小白的想法是:将![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的对称轴进行翻折,即作
的对称轴进行翻折,即作![]() 交
交![]() 的延长线于
的延长线于![]() (如图3)
(如图3)
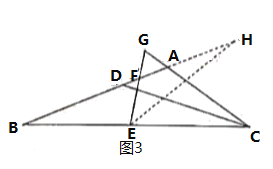
经验拓展:等边![]() 中,
中,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长(用含
的长(用含![]() ,
,![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目: 来源: 题型:
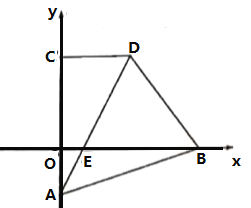
【题目】平面直角坐标系中,点![]() 坐标为
坐标为![]() ,
,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正半轴上一点,过点
轴正半轴上一点,过点![]() 作
作![]() 轴,
轴,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,连接
,连接![]() .
.
(1)请通过计算说明![]() ;
;
(2)求证![]() ;
;
(3)请直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目: 来源: 题型:
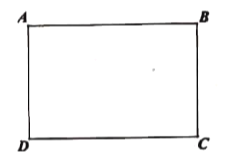
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发(不含点
出发(不含点![]() )以
)以![]() 的速度沿
的速度沿![]() 的方向运动到点
的方向运动到点![]() 停止,点
停止,点![]() 出发
出发![]() 后,点
后,点![]() 才开始从点
才开始从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 的方向运动到点
的方向运动到点![]() 停止,当点
停止,当点![]() 到达点
到达点![]() 时,点
时,点![]() 恰好到达点
恰好到达点![]() .
.
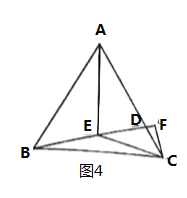
(1)当点![]() 到达点
到达点![]() 时,
时,![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(2)在(1)的条件下,设点![]() 运动时间为
运动时间为![]() ,运动过程中
,运动过程中![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示面积
的式子表示面积![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学兴趣小组在“用面积验证平方差公式”时,经历了如下的探究过程;
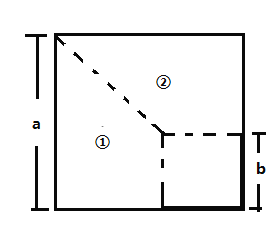
(1)小明的想法是:将边长为![]() 的正方形右下角剪掉一个边长为
的正方形右下角剪掉一个边长为![]() 的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
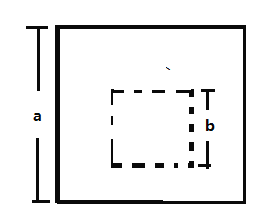
(2)小白的想法是:在边长为![]() 的正方形内部任意位置剪掉一个边长为
的正方形内部任意位置剪掉一个边长为![]() 的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com