
科目: 来源: 题型:
【题目】 如图,已知A(-1,2),B(-3,1),C(-4,3).
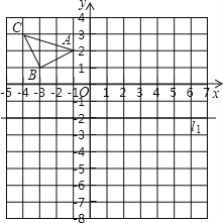
(1)作△ABC关于x轴的对称图形△A1B1C1,写出点C关于x轴的对称点C1的坐标;
(2)作△ABC关于直线l1:y=-2(直线l1上各点的纵坐标都为-2)的对称图形△A2B2C2,写出点C关于直线l1的对称点C2的坐标.
(3)作△ABC关于直线l2:x=1(直线l2上各点的横坐标都为1)的对称图形△A3B3C3,写出点C关于直线l2的对称点C3的坐标.
(4)点P(m,n)为坐标平面内任意一点,直接写出:
点P关于直线x=a(直线上各点的横坐标都为a)的对称点P1的坐标;
点P关于直线y=b(直线上各点的纵坐标都为b)的对称点P2的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】 已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,∠C=∠C′=90°.求证:Rt△ABC和Rt△A′B′C′全等.
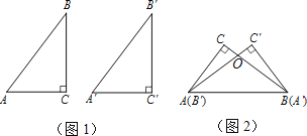
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)如图2,将△ABC和A′B′C′拼在一起(即:点A与点B′重合,点B与点A′重合),BC和B′C′相交于点O,请用此图证明上述命题.
查看答案和解析>>
科目: 来源: 题型:
【题目】 小明遇到这样一个问题
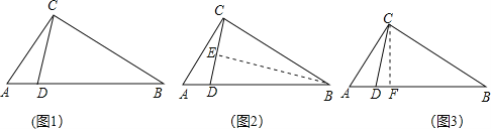
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )
,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1. 正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】 如图,“复兴一号“水稻的实验田是边长为m米的正方形去掉一个边长为n米(m>n)正方形蓄水池后余下的部分,“复兴二号“水稻的试验田是边长为(m-n)米的正方形,两块试验田的水稻都收获了a千克.
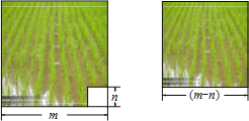
(1)哪种水稻的单位面积产量高?为什么?
(2)高的单位面积产量比低的单位面积产量高多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】 如图,先将正方形纸片对折,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点E在CB上,点B在MN上的对应点为H,连接DH,则下列选项错误的是( )
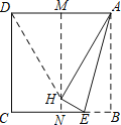
A.△ADH是等边三角形B.NE=![]() BC
BC
C.∠BAE=15°D.∠MAH+∠NEH=90°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )

A. 9cm B. 12cm C. ![]() cm D. 18cm
cm D. 18cm
查看答案和解析>>
科目: 来源: 题型:
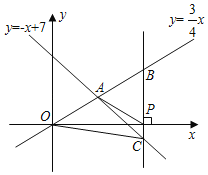
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
x与一次函数y=﹣x+7的图象交于点A,x轴上有一点P(a,0).
(1)求点A的坐标;
(2)若△OAP为等腰三角形,则a= ;
(3)过点P作x轴的垂线(垂线位于点A的右侧)、分别交y=![]() x和y=﹣x+7的图象于点B、C,连接OC.若BC=
x和y=﹣x+7的图象于点B、C,连接OC.若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.
查看答案和解析>>
科目: 来源: 题型:
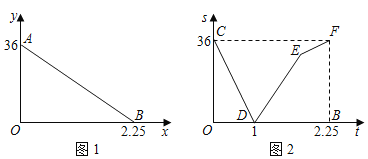
【题目】小明从家出发沿一条笔直的公路骑自行车前往图书馆看书,他与图书馆之间的距离y(km)与出发时间t(h)之间的函数关系如图1中线段AB所示,在小明出发的同时,小明的妈妈从图书馆借书结束,沿同一条公路骑电动车匀速回家,两人之间的距离s(km)与出发时间t(h)之间的函数关系式如图2中折线段CD﹣DE﹣EF所示.
(1)小明骑自行车的速度为 km/h、妈妈骑电动车的速度为 km/h;
(2)解释图中点E的实际意义,并求出点E的坐标;
(3)求当t为多少时,两车之间的距离为18km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com