
科目: 来源: 题型:
【题目】综合与实践
已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
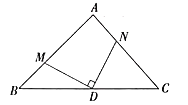
(1)如图:过![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() .求证:
.求证:![]() .
.
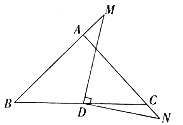
(2)如图,若![]() ,分别与
,分别与![]() 、
、![]() 的延长线交于点
的延长线交于点![]() 、
、![]() ,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.
,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了________度,线段CE旋转过程中扫过的面积为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成相应的任务.
基本性质:三角形中线等分三角形的面积.
如图,![]() 是
是![]() 的边
的边![]() 上的中线,
上的中线,
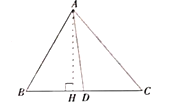
则![]()
理由:过点![]() 作
作![]() 于点
于点![]()
∵![]() 是
是![]() 的边
的边![]() 上的中线.
上的中线.
∴![]() 又∵
又∵![]() ,
,![]()
∴![]()
∴三角形中线等分三角形的面积.
任务:
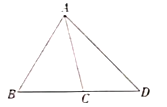
(1)如图,延长![]() 的边
的边![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,则
,则![]() 和
和![]() 的数量关系为_________.
的数量关系为_________.
(2)如图,点![]() 是
是![]() 的边
的边![]() 上任意一点,点
上任意一点,点![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() 的面积为
的面积为![]() ,请同学们借助上述结论求
,请同学们借助上述结论求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )

A. 当BC等于0.5时,l与⊙O相离
B. 当BC等于2时,l与⊙O相切
C. 当BC等于1时,l与⊙O相交
D. 当BC不为1时,l与⊙O不相切
查看答案和解析>>
科目: 来源: 题型:
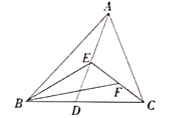
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知反比例函数y=![]() (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1、x2)、B(x2、y2),当y1>y2时,试比较x1与x2的大小;
(4)若在其图象上任取一点,向x轴和y轴作垂线,若所得矩形面积为6,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某陶瓷公司招工广告称:“本公司工人工作时间:每天工作![]() 小时,每月工作
小时,每月工作![]() 天;待遇:工人按计件付工资,每月另加生活费
天;待遇:工人按计件付工资,每月另加生活费![]() 元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
甲种陶瓷 (单位:个) | 乙种陶瓷 (单位:个) | 总时间 (单位:分钟) | 计件工资 (单位:元) |
|
|
|
|
|
|
|
|
(1)设生产每个甲种陶瓷所需的时间为![]() 分钟,用含有
分钟,用含有![]() 的代数式表示生产每个乙种陶瓷所需的时间;
的代数式表示生产每个乙种陶瓷所需的时间;
(2)设小王工人小王某月(工作![]() 天)生产甲种陶瓷
天)生产甲种陶瓷![]() 个,乙种陶瓷
个,乙种陶瓷![]() 个,
个,
①试求![]() 与
与![]() 的函数关系式;(不需写出自变量
的函数关系式;(不需写出自变量![]() 的取值范围)
的取值范围)
②根据市场调查,每个工人每月生产甲种陶瓷的数量不少于乙种陶瓷数量的![]() 倍,且生产每个乙种陶瓷的计件工资可提高
倍,且生产每个乙种陶瓷的计件工资可提高![]() 元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资
元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资![]() 月工资)才能领到
月工资)才能领到![]() 元?
元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 的顶点都在正方形网格的格点上,点
的顶点都在正方形网格的格点上,点![]()
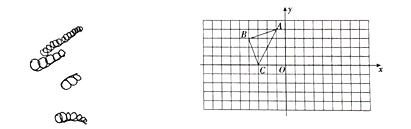
(1)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为___________.
的坐标为___________.
(2)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为__________.
的坐标为__________.
(3)观察图形,说一说点![]() 和点
和点![]() 的坐标有什么特点.
的坐标有什么特点.
查看答案和解析>>
科目: 来源: 题型:
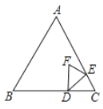
【题目】如图,等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 方向向点
方向向点![]() 运动,
运动,![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 上;
上;
(2)当![]() 时,求
时,求![]() 与
与![]() 的数量关系;
的数量关系;
(3)当点![]() 、
、![]() 、
、![]() 三点共线时,求证:点
三点共线时,求证:点![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com