
科目: 来源: 题型:
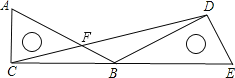
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD.
(1)试判断△CBD的形状,并说明理由;
(2)求∠BDC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=-x2-2x+3.
(1)将其配方成y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标.
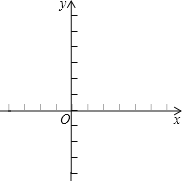
(2)在平面直角坐标系中画出函数的图象,并观察图象,当y≥0时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们已经知道,形如![]() 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:
例如: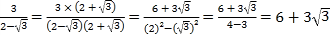 。
。
下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:![]() 该如何化简?
该如何化简?
建立模型:形如![]() 的化简,只要我们找到两个数
的化简,只要我们找到两个数![]() ,使
,使![]() ,这样
,这样![]() ,
,![]() ,那么便有:
,那么便有:![]() ,
,
问题解决:化简![]() ,
,
解:首先把![]() 化为
化为![]() ,这里
,这里![]() ,
,![]() ,由于4+3=7,
,由于4+3=7,![]() ,
,
即(![]() ,
,![]() ,
,
∴![]()
模型应用1:
利用上述解决问题的方法化简下列各式:
(1)![]() ;(2)
;(2)![]() ;
;
模型应用2:
(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。
查看答案和解析>>
科目: 来源: 题型:
【题目】一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 之间的函数关系。
之间的函数关系。
根据图象回答下列问题:

(1)甲地与乙地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需_______小时,普通列车的速度是______千米/小时;
(3)动车的速度是________千米/小时;
(4)![]() 的值为________.
的值为________.
查看答案和解析>>
科目: 来源: 题型:
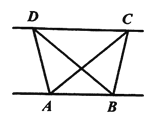
【题目】(1)探究新知:如图1,已知![]() 与
与![]() 的面积相等,试判断
的面积相等,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)结论应用:
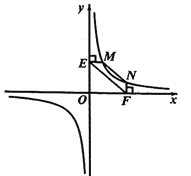
①如图2,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图像上,过点
的图像上,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() .试证明:
.试证明:![]() .
.
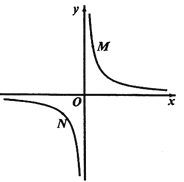
②若①中的其他条件不变,只改变点![]() ,
,![]() 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,正方形
,正方形![]() 的边
的边![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
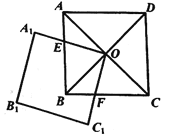
(1)求证:![]() ;
;
(2)如果正方形![]() 的边长为
的边长为![]() ,那么正方形
,那么正方形![]() 绕
绕![]() 点转动的过程中,与正方形
点转动的过程中,与正方形![]() 重叠部分的面积始终等于__________.(用含
重叠部分的面积始终等于__________.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
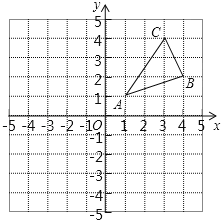
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
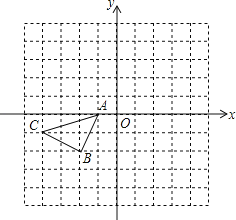
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
查看答案和解析>>
科目: 来源: 题型:
【题目】为了倡导“全民阅读”,某校为调查了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成统计图表如下:
学生家庭藏书情况扇形统计图

类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息,解答下列问题:
(1)共抽样调查了______名学生,![]() ______;
______;
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为_______
”对应扇形的圆心角为_______![]() ;
;
(3)若该校有2000名学生,请估计全校学生中家庭藏书超过60本的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com