
科目: 来源: 题型:
【题目】问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观, 从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形积的方法进行直 观推导和解释.

![]() 如图 1,是一个重要公式的几何解释,请你写出这个公式:
如图 1,是一个重要公式的几何解释,请你写出这个公式:
![]() 如图 2,在
如图 2,在![]() 中,
中,![]() ,以
,以![]() 的三边长向外作正方形的面积分别为
的三边长向外作正方形的面积分别为![]() ,试猜想
,试猜想![]() 之间存在的等量关系,直接写出结论 .
之间存在的等量关系,直接写出结论 .
![]() 如图 3,如果以
如图 3,如果以![]() 的三边长
的三边长![]() 为直径向外作半圆,那么第
为直径向外作半圆,那么第![]() 问的结论 是否成立?请说明理由.
问的结论 是否成立?请说明理由.
![]() 如图 4,在
如图 4,在![]() 中,
中,![]() ,三边分别为
,三边分别为![]() ,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
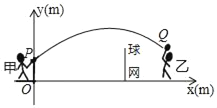
【题目】甲、乙两人进行羽毛球比赛,把球看成点,其飞行的路线为抛物线的一部分.如图建立平面直角坐标系,甲在O点正上方1m的P处发球,羽毛球飞行的高度y(m)与羽毛球距离甲站立位置(点O)的水平距离x(m)之间满足函败表达式y=a(x﹣4)2+h.已知点O与球网的水平距离为5m,球网的高度为1.55m,球场边界距点O的水平距离为10m.
(1)当a=﹣![]() 时,求h的值,并通过计算判断此球能否过网.
时,求h的值,并通过计算判断此球能否过网.
(2)若甲发球过网后,乙在另一侧距球网水平距离lm处起跳扣球没有成功,球在距球网水平距离lm,离地面高度2.2m处飞过,通过计算判断此球会不会出界?
查看答案和解析>>
科目: 来源: 题型:
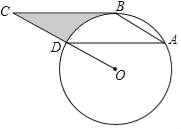
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的文字,解答问题大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来, 而由于
的小数部分我们不可能全部地写出来, 而由于![]() ,所以
,所以![]() 的整数部分为
的整数部分为![]() ,将 减去其整数部分
,将 减去其整数部分![]() ,所得的差就是其小数部分
,所得的差就是其小数部分![]() ,根据以上内容,解答下面的问题:
,根据以上内容,解答下面的问题:
![]()
![]() 的整数部分是 ;小数部分是 .
的整数部分是 ;小数部分是 .
![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
![]() 若设
若设![]() 整数部分为
整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
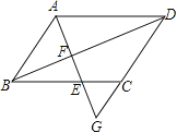
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是
A. 连续抛一均匀硬币2次必有1次正面朝上
B. 连续抛一均匀硬币10次都可能正面朝上
C. 大量反复抛一均匀硬币,平均100次出现正面朝上50次
D. 通过抛一均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

查看答案和解析>>
科目: 来源: 题型:
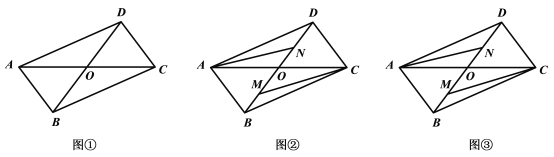
【题目】如图①所示,![]() 是某公园的平面示意图,
是某公园的平面示意图,![]() 分别是该公园的四个入口,两条主干道
分别是该公园的四个入口,两条主干道![]() 交于点
交于点![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,请你帮助公园的管理人员解决以下问题:
,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 ![]() ;
;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() (点
(点![]() 与点
与点![]() 不重合),并计划在
不重合),并计划在![]() 与
与![]() 两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你画出该公园修建这三条绿道投入资金最小值时的图形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知m,n(m<n)是关于x的方程(x–a)(x–b)=2的两根,若a<b,则下列判断正确的是
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com