
科目: 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践 问题情境:
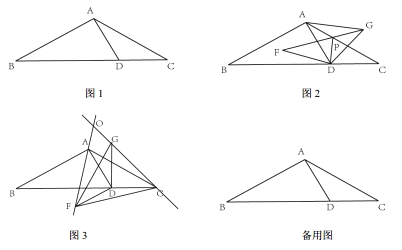
综合与实践课上,同学们以“三角形纸片的折叠与旋转“为主题展开数学活动,探究有关的数学问题.
动手操作:
已知:三角形纸片![]() 中,
中,![]() .将三角形纸片
.将三角形纸片![]() 按如下步骤进行操作:
按如下步骤进行操作:
第一步:如图1,折叠三角形纸片![]() ,使点
,使点![]() 与点
与点![]() 重合,然后展开铺平,折痕分别交
重合,然后展开铺平,折痕分别交![]() 于点
于点![]() ,连接
,连接![]() ,易知
,易知![]() .
.
第二步:在图1的基础上,将三角形纸片![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 的位置不变,将
的位置不变,将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() (点
(点![]() 分别是
分别是![]() 的对应点),旋转角为
的对应点),旋转角为![]() 问题解决:
问题解决:
(1)如图2,小彬画出了旋转角![]() 时的图形,设线段
时的图形,设线段![]() 交于点
交于点![]() ,连接
,连接![]() .小彬发现
.小彬发现![]() 所在直线始终垂直平分线段
所在直线始终垂直平分线段![]() .请证明这一结论;
.请证明这一结论;
(2)如图3,小颖画出了旋转角![]() 时的图形,设直线
时的图形,设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() 判断此时
判断此时![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 绕点
绕点![]() 逆时针旋转过程中,当
逆时针旋转过程中,当![]() 时,请直接写出
时,请直接写出![]() 两点间的距离.
两点间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】近日,中国工程院院士、“杂交水稻之父”袁隆平团队选育培植的耐盐碱水稻(即海水稻)在山东青岛等六个试验基地开始春播育秧,预计今年的种植规模将超一万亩.已知去年某基地甲、乙两块实验田海水稻的总产量都是3600千克,乙实验田海水稻种植面积是甲实验田的![]() ,而乙实验田海水稻平均亩产量比甲多60千克.
,而乙实验田海水稻平均亩产量比甲多60千克.
(1)求甲、乙两块实验田种植海水稻的面积;
(2)经过科学家的努力,海水稻正从试验田走向餐桌,某电商新购进A、B两种包装的海水稻产品共50袋,其进价、标价及优惠方案如下表所示.若要保证这批海水稻产品全部售出后所得利润不少于1000元,该电商至少要购进A种包装的海水稻产品多少袋?
包装类型 | A | B |
进价(元/袋) | 100 | 30 |
标价(元/袋) | 150 | 50 |
优惠方案 | 全部九折 | |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A(1,2)、B(–1,–2)是函数![]() 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则( )
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则( )
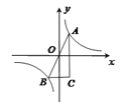
A. S = 2 B. S = 4 C. S = 8 D. S = 1
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“过一点作已知直线的垂线”的尺规作图过程,请你阅读后完成相应任务,如图,已知直线![]() 及上一点
及上一点![]() .求作:直线
.求作:直线![]() ,使
,使![]() 于点
于点![]() .
.
作法:①在直线![]() 外任取一点
外任取一点![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() (不与点
(不与点![]() 重合)③作射线
重合)③作射线![]() ,交①中所画的弧于点
,交①中所画的弧于点![]() ;④作直线
;④作直线![]() ,直线
,直线![]() 就是所求作的直线
就是所求作的直线![]() 的垂线.
的垂线.
任务:(1)根据小明设计的尺规作图过程,补全图形(要求:尺规作图,保留作图痕迹);
(2)证明上述方法得到的直线![]() 直线
直线![]() .
.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
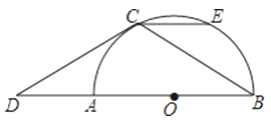
【题目】如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
(1)求∠D的度数;
(2)求证:以点C,O,B,E为顶点的四边形是菱形.
查看答案和解析>>
科目: 来源: 题型:
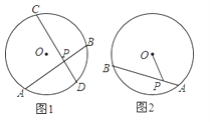
【题目】九年级学生小刚是一个喜欢看书的好学生,他在学习完第二十四章圆后,在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来就是:PAPB=PCPD,小刚很想知道是如何证明的,可异证明部分污损看不清了,只看到辅助线的做法,分别连结AC、BD.聪明的你一定能帮他证出,请在图1中做出辅助线,并写出详细的证明过程.
小刚又看到一道课后习题,如图2,AB是⊙O弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径,愁坏了小刚,乐于助人的你肯定会帮助他,请写出详细的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com