
科目: 来源: 题型:
【题目】已知:如图,直线![]() 的函数解析式为
的函数解析式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
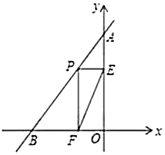
(1)直接写出点![]() 的坐标________;
的坐标________;![]() 点的坐标________;
点的坐标________;
(2)若点![]() 为线段
为线段![]() 上的一个动点,作
上的一个动点,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,问:①若
,问:①若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;②直接写出
的函数关系式;②直接写出![]() 的最小值________;
的最小值________;
查看答案和解析>>
科目: 来源: 题型:
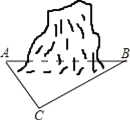
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目: 来源: 题型:
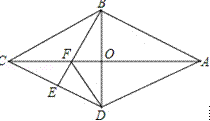
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为 60°,然后在坡顶D测得树顶B的仰角为300,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( ) m

A. ![]() B. 30 C.
B. 30 C. ![]() D. 40
D. 40
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
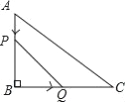
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017浙江省台州市)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
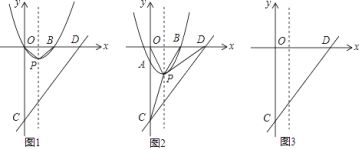
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n即为该方程的另一个实数根.
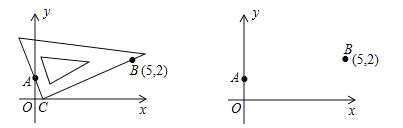
(1)在图2中,按照“第四步”的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的m就是方程![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程![]() (a≠0,
(a≠0,![]() ≥0)的实数根,请你直接写出一对固定点的坐标;
≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当m1,n1,m2,n2与a,b,c之间满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),直线![]() 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8![]() ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
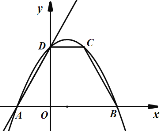
图(1)
(1) 求抛物线的解析式;
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与![]() 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
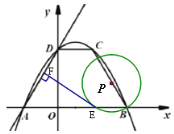
图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
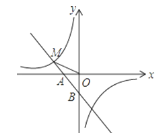
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)求△MOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
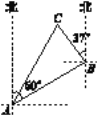
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com