
科目: 来源: 题型:
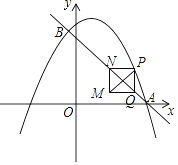
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
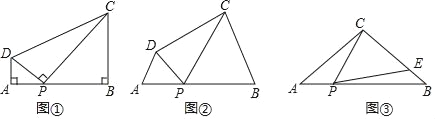
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
查看答案和解析>>
科目: 来源: 题型:
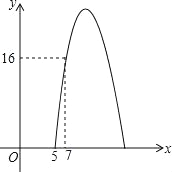
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
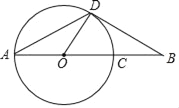
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与![]() 围成的扇形的面积.
围成的扇形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线所对应的二次函数的表达式.
(2)直接写出该抛物线开口方向和顶点坐标.
(3)直接在所给坐标平面内画出这条抛物线.
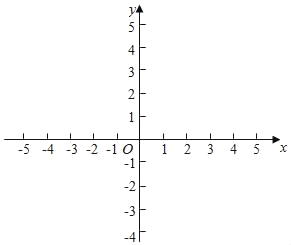
查看答案和解析>>
科目: 来源: 题型:
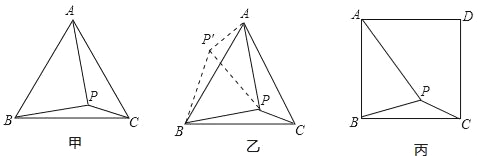
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】四张小卡片上分别写有数字1、2、3、4,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字3的概率;
(2)随机地从盒子里抽取一张,将数字记为x,不放回再抽取第二张,将数字记为y,请你用画树状图或列表的方法表示所有等可能的结果,并求出点(x,y)在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com