
科目: 来源: 题型:
【题目】定义:如果M个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M个数的自然数组,如(3,6)为两个数的自然数组,因为(3×6)能被(3+6)整除;又如(15,30,60)为三个数的自然数组,因为(15×30)能被(15+30)整除,(15×60)能被(15+60)整除,(30×60)能被(30+60)整除…
(1)求证:2n和n(n﹣2)(n≥3,n为整数)组成的数组是两个数的自然数组;
(2)若(4a,5a,6a)是三个数的自然数组,求满足条件的三位正整数a,并判断(4a+5,5a+5,6a+5)是否为自然数组.
查看答案和解析>>
科目: 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,AB=BC,E、M分别为AB、AC上的点,连接CE,BM交于点G,且BM⊥CE,O为AC的中点,连接BO交CE于点N.
(1)如图①,若AB=6,2MO=AM,求BM的长;
(2)如图②,连接OG、AG,若AG⊥OG,求证:AC=![]() BG.
BG.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=
(x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=![]()
(1)求一次函数及反比例函数的表达式;
(2)将一次函数图象向下平移,使其经过原点O,与反比例函数图象在第四象限内的交点为A,连接AC,求四边形OACB的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,巫溪中学对部分学生就校园安全知识的了解程度, 采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分对应扇形的圆心角为 度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生,2名女生,达到“不了解”程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”程度的人中分别抽取1人参加校园知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线y=![]() x2﹣
x2﹣![]() x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D

(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
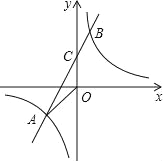
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目: 来源: 题型:
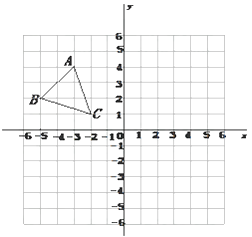
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目: 来源: 题型:
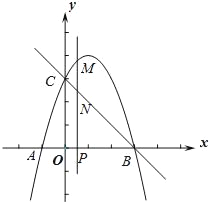
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com