
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点A(-1,0),B(1,4),C(0,3).
(1)求出此二次函数的表达式,并把它化成![]() 的形式;
的形式;
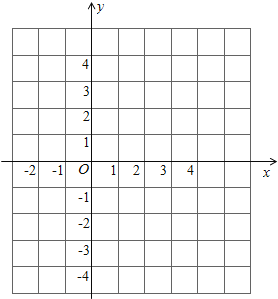
(2)请在坐标系内画出这个函数的图象,并根据图象写出函数值y为负数时,自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
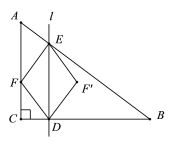
【题目】如图,在Rt△ABC中, ![]() ,
,![]() ,
,![]() ,直线l从与AC重合的位置开始以每秒
,直线l从与AC重合的位置开始以每秒![]() 个单位的速度沿CB方向平行移动,且分别与CB,AB边交于D,E两点,动点F从A开始沿折线AC
个单位的速度沿CB方向平行移动,且分别与CB,AB边交于D,E两点,动点F从A开始沿折线AC![]() CB
CB![]() BA运动,点F在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位,点F与直线l同时出发,设运动的时间为t秒,当点F第一次回到点A时,点F与直线 l同时停止运动.运动过程中,作点F关于直线DE的对称点,记为点
BA运动,点F在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位,点F与直线l同时出发,设运动的时间为t秒,当点F第一次回到点A时,点F与直线 l同时停止运动.运动过程中,作点F关于直线DE的对称点,记为点![]() ,若形成的四边形
,若形成的四边形![]() 为菱形,则所有满足条件的
为菱形,则所有满足条件的![]() 之和为_________.
之和为_________.
查看答案和解析>>
科目: 来源: 题型:
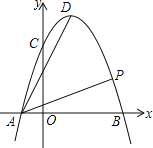
【题目】如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,则点P的坐标为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数的图象如下所示,下列5个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的实数),其中正确的结论有几个?
的实数),其中正确的结论有几个?
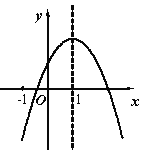
A. ①②③ B. ②③④ C. ②③⑤ D. ③④⑤
查看答案和解析>>
科目: 来源: 题型:
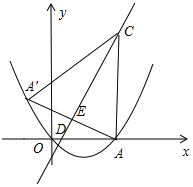
【题目】如图所示,抛物线y=ax2-![]() x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x-2于点C,且直线y=2x-2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x-2于点C,且直线y=2x-2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x-2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
查看答案和解析>>
科目: 来源: 题型:
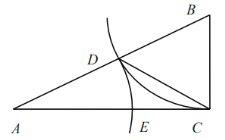
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
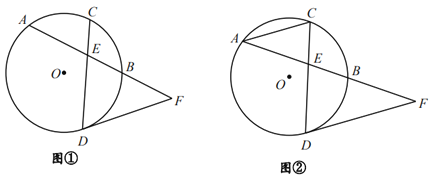
【题目】如图,已知,⊙O的半径![]() ,弦AB,CD交于点E,C为
,弦AB,CD交于点E,C为![]() 的中点,过D点的直线交AB延长线与点F,且DF=EF.
的中点,过D点的直线交AB延长线与点F,且DF=EF.
(1)如图①,试判断DF与⊙O的位置关系,并说明理由;
(2)如图②,连接AC,若AC∥DF,BE=![]() AE,求CE的长.
AE,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
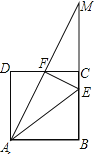
【题目】如图,正方形ABCD中,点E在BC上,且CE=![]() BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=
BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=![]() S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
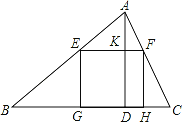
【题目】如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设EG=x mm,EF=y mm.
(1)写出x与y的关系式;
(2)用S表示矩形EGHF的面积,某同学说当矩形EGHF为正方形时S最大,这个说法正确吗?说明理由,并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com