
科目: 来源: 题型:
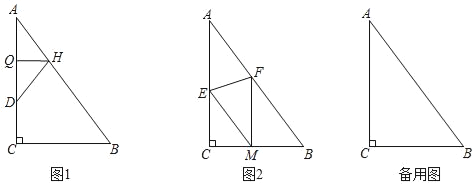
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若S△ABC=9S△DHQ,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥AC,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=![]() (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣![]() t2+5t﹣
t2+5t﹣![]() )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣![]() t2+3t﹣
t2+3t﹣![]() )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣![]() x2+bx+c的顶点.
x2+bx+c的顶点.
①当点P在双曲线y=![]() 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=![]() 没有公共点;
没有公共点;
②当抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某书店参加某校读书活动,并为每班准备了A,B两套名著,赠予各班甲、乙两名优秀读者,以资鼓励.某班决定采用游戏方式发放,其规则如下:将三张除了数字2,5,6不同外其余均相同的扑克牌,数字朝下随机平铺于桌面,从中任取2张,若牌面数字之和为偶数,则甲获A名著;若牌面数字之和为奇数,则乙获得A名著,你认为此规则合理吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
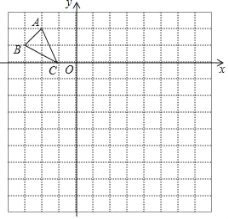
【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中建立平面直角坐标系,格点△ABC(顶点是网格线的交点)的坐标分别是A(﹣2,2),B(﹣3,1),C(﹣1,0).
(1)将△ABC绕点O逆时针旋转90°得到△DEF,画出△DEF;
(2)以O为位似中心,将△ABC放大为原来的2倍,在网格内画出放大后的△A1B1C1,若P(x,y)为△ABC中的任意一点,这次变换后的对应点P1的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

查看答案和解析>>
科目: 来源: 题型:
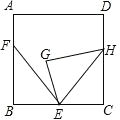
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com